题目内容
【题目】已知二次函数y=ax2+bx+c(a<0)的图象经过(m+1,a),(m,b)两点.
(1)若m=1,a=-1,求该二次函数的解析式;
(2)求证:am+b=0;
(3)若该二次函数的最大值为![]() ,当x=1时,y≥3a,求a的取值范围.
,当x=1时,y≥3a,求a的取值范围.
【答案】(1)y=-x2+x+1;(2)证明见解析;(3)![]() .
.
【解析】
(2)把m=1,a=-1代入(m+1,a),(m,b)得(2,-1),(1,b),把(2,-1),(1,b)代入函数解析式,进行解方程组即可;
(2)把(m+1,a),(m,b)代入函数解析式,得到方程组,将方程组进行整理即可;
(3)由(2)得的方程组可得:c=b=-am.即可得出抛物线解析式为:y=ax2-amx-am.当x=1时,得到不等式:a-am-am≥3a,解得 m≥-1. 利用最值得到方程![]() ,整理得:
,整理得:![]() .将c=b=-am代入,解得:
.将c=b=-am代入,解得:![]() =
=![]() =
=![]() .进行解答即可.
.进行解答即可.
解:(1)若m=1,a=-1,则抛物线y=-x2+bx+c过 (2,-1),(1,b) 两点,
∴![]()
解得![]()
∴这个二次函数的解析式为y=-x2+x+1.
(2)∵抛物线y=ax2+bx+c经过(m+1,a),(m,b)两点,
∴ 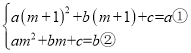
①-②,得 2am+a+b=a-b.
整理,得 am+b=0;
(3)由(2)得,b=-am,代入②,得c=b=-am.
∴y=ax2-amx-am.
∵当x=1时,y≥3a,
∴a-am-am≥3a,即-2am≥2a,
∵a<0,∴m≥-1.
∵该二次函数的最大值为![]() ,
,
∴![]() ,即
,即![]() .③
.③
将c=b=-am代入③,得![]() ,
,
∴![]() =
=![]() =
=![]() .
.
∵m≥-1,
∴![]() ≥-3,
≥-3,
∵a<0
∴a≤![]() .
.

练习册系列答案
相关题目