Question

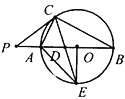
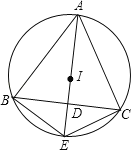
【题目】如图，点I是△ABC的内心，A的延长线交边BC于点D，交△ABC外接圆于点E．求证：IE＝BE＝CE．

Answer 1

【答案】见解析

【解析】

连接BI，由三角形的内心的性质可得∠BAE＝∠CAE，∠ABI＝∠CBI，由圆周角定理可得∠BAE＝∠CBE＝∠CAE＝∠BCE，可得BE＝CE，由外角的性质可得∠BIE＝∠IBE，IE＝BE，即可得结论；

证明：连接BI，

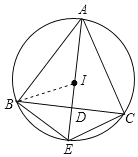
∵点I是△ABC的内心，

∴∠BAE＝∠CAE，∠ABI＝∠CBI，

∵∠CBE＝∠CAE，∠BCE＝∠BAE，

∴∠BAE＝∠CBE＝∠CAE＝∠BCE，

∴BE＝CE

∵∠BIE＝∠ABI+∠BAE，∠IBE＝∠CBI+∠CBE，

∴∠BIE＝∠IBE，

∴IE＝BE，

∴IE＝BE＝CE；