Question

【题目】如图，AB为⊙O的直径，AC，BC是⊙O的两条弦，过点C作∠BCD=∠A，CD交AB的延长线与点D．

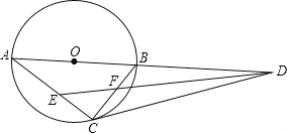
（1）求证：CD是⊙O的切线；

（2）若tanA=，求的值；

（3）在（2）的条件下，若AB=7，∠CED=∠A+∠EDC，求EC与ED的长．

Answer 1

【答案】（1）见解析；（2）=；（3）EC=，DE=．

【解析】

（1）连接OC，由∠A=∠1=∠2且∠2+∠OCB=90°知∠1+∠OCB=90°，据此即可得证；
（2）先△ADC∽△CDB得且CD2=ADBD，设CD=4x，CA=4k，知AB=5k，从而得出（4x）2=3x（3x+5k），可得k，进而得出答案；

（3）由（2）得AB=7、BD=9、CD=12，证DE是∠ADC的平分线知证得∠A+∠EDA=∠DEC=45°，作DH⊥AC，知△CDH为等腰直角三角形，由BC∥DH知∠CDH=∠1，据此得继而得

（1）如图，连接OC，

∵OA=OC，

∴∠A=∠2，

∵∠A=∠1，

∴∠1=∠2，

∵AB是⊙O的直径，

∴∠ACB=90°，即∠2+∠OCB=90°，

∴∠1+∠OCB=90°，即∠OCD=90°，

∴CD是⊙O的切线；

（2）∵∠1=∠A，∠ADC=∠ADC，

∴△ADC∽△CDB，

∵tanA==，

∴==，

∴=ADBD，

设CD=4x，CA=4k，

则AB=5k，

∴=3x（3x+5k），

解得x=k，BD=k，

∴==；

（3）由（2）知AB=5k=7知k=，

则BD=9，CD=4x=4×k=4××=12，

∵∠CED=∠A+∠EDC=∠A+∠ADE，

∴∠EDC=∠ADE，即DE是∠ADC的平分线，

∴===，

则AC=7×=，

∴EC=×=，

∵∠1=∠A，∠EDA=∠EDC，且∠A+∠1+∠EDA+∠EDC=90°，

∴∠A+∠EDA=∠DEC=45°，

过点D作DH⊥AC交AC延长线于点H，

则△CDH为等腰直角三角形，

∵BC∥DH，

∴∠CDH=∠1，

∴tan∠CDH==，

∴DH=CD=12×=，

则DE=DH=．