Question

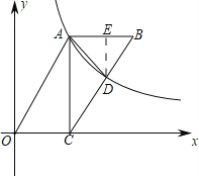
【题目】如图，已知抛物线经过，及原点，顶点为．

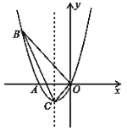
（1）求抛物线的函数解析式；

（2）设点在抛物线上，点在抛物线的对称轴上，且以、、，为顶点，为边的四边形是平行四边形，求点的坐标；

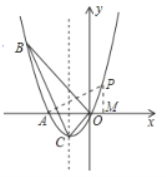
（3）是抛物线上第一象限内的动点，过点作轴，垂足为．是否存在这样的点，使得以，，为顶点的三角形与相似？若存在，求出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）点的坐标为：（1，3）；（3）存在．符合条件的点有两个，分别是或（3，15）．

【解析】

（1）由于抛物线经过A（-2，0），B（-3，3）及原点O，待定系数法即可求出抛物线的解析式；
（2）根据平行四边形的性质，对边平行且相等，可以求出点D的坐标；
（3）分两种情况讨论，①△AMP∽△BOC，②PMA∽△BOC，根据相似三角形对应边的比相等可以求出点P的坐标．

解：（1）设抛物线的解析式为，将点，，代入，可得：

，

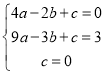解得：．

故函数解析式为：；

（2）当AO为平行四边形的边时，DE∥AO，DE=AO，

由A（-2，0）知：DE=AO=2，
由四边形AODE可知D在对称轴直线x=-1右侧，
则D横坐标为1，代入抛物线解析式得D（1，3）．
综上可得点D的坐标为：（1，3）；

（3）存在．理由如下：

如图：，，

根据勾股定理得：，

，

，

，

是直角三角形，，

假设存在点，使以，，为顶点的三角形与相似，

设，由题意知，，且，

①若，则，即，

得：，（舍去）．

当时，，即,

②若，则，

即：，

得：，（舍去），

当时，，即．

故符合条件的点有两个，分别是或（3，15）．