题目内容
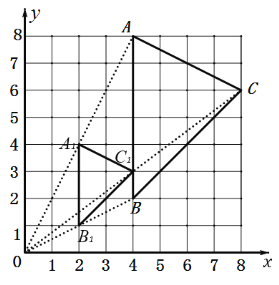
【题目】如图，在平面直角坐标系中，△ABC 的顶点坐标分别为A(4，8)，B(4，2)，C(8，6) ．
（1）在第一象限内，画出以原点O 为位似中心，与△ABC 的相似比为
的△A1B1C1，并写出 A1，C1点的坐标；
（2）如果△ABC 内部一点P的坐标为 (x， y) ，写出点P在△A1B1C1内的对应点 P1 的坐标．
【答案】（1）见解析；
（2，4），
（4，3）；（2）
（
，
）．
【解析】
(1)直接利用位似图形的性质得出对应点位置进而得出答案；
(2)利用位似图形的性质，即可得出答案．
(1)如图，连接OA、OB、OC，分别取它们的中点A1、B1、C1，
三角形A1B1C1即为所求．(2，4)，(4，3)；
(2)∵△ABC内部一点P的坐标为
，
∴点P在△A1B1C1内的对应点P1的坐标为(，)
练习册系列答案
相关题目
【题目】已知抛物线y＝ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表：
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式；
(2)已知点E(4， y)是该抛物线上的点，点E关于抛物线的对称轴对称的点为点F，求点E和点F的坐标．
