Question

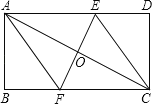
【题目】已知如图，矩形ABCD的周长为64，AB=12，对角线AC的垂直平分线分别交AD、BC于E、F，连接AF、CE、EF，且EF与AC相交于点O．

（1）求证：四边形AECF是菱形；

（2）求S△ABF与S△AEF的比值．

Answer 1

【答案】（1）证明见解析；（2）8：17．

【解析】

（1）根据SSS证明△AOE≌△COF，根据全等得出OE=OF，推出四边形是平行四边形，再根据EF⊥AC即可推出四边形是菱形；
（2）由（1）知S△AEF=S△ACF，再分别求得S△ABF与S△AEF的面积即可得到其比值．

（1）∵四边形ABCD是矩形，

∴AD∥BC，

∴∠OAE=∠OCF．

∵EF垂直平分AC，

∴AO=CO，∠AOE=∠COF=90°，

∴△AOE≌△COF(ASA)，

∴OE=OF，

∴四边形AFEC是平行四边形，

又∵EF⊥AC，

∴四边形AFEC是菱形；

（2）∵△AOE≌△COF，

∴S△AEF=S△ACF

∵S△ABF=3BF，S△AEF=3FC，

∴S△ABF：S△AEF=BF：FC．

∵矩形ABCD的周长为64，AB=12，

∴BC=20，

设FC=x，则AF=x，BF=20﹣x

在Rt△ABF中，由勾股定理

　122+(20﹣x)2=x2

解得：x，

BF，

∴S△ABF：S△AEF=BF：FC=8：17．