题目内容
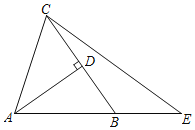
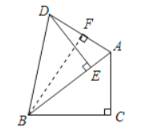
【题目】如图，Rt△ABC中，∠C=90°，把R△ABC绕着B点逆时针旋转，得到Rt△DBE，点E在AB上 .
(1)若∠BDA=70°，求∠BAC的度数；
(2)若BC=8，AC=6，求△ABD中AD边上的高.
【答案】（1）50° （2）
【解析】
（1）由旋转性质知BD=BA，∠CBA=∠EBD，据此可得∠BDA=70°，从而得∠ABD=∠ABC=40°，结合∠C=90°可得答案；
（2）由旋转性质得BE=BC=8，DE=AC=6，AB=BD=10，从而得AE=2，利用勾股定理知AD=
，作BF⊥AD于点F得AF=
AD=
，再次利用勾股定理可得答案．
解：(1)由旋转性质知BD=BA，∠CBA=∠EBD，
∵∠BDA=70°，
∴∠BAD=70°，
∴∠ABD=∠ABC=40°，
∵∠C=90°，
∴∠BAC=50°；
(2)∵BC=8，AC=6，∠C=90°，
∴AB=
=
=10，
由旋转性质知△ABC≌△DBE，
则BE=BC=8，DE=AC=6，AB=BD=10
∴AE=AB-BE=2，
在Rt△ADE中，AD=
作BF⊥AD于点F，
∵BA=BD，
∴AF=AD=
∴BF=
练习册系列答案
名校联盟快乐课堂系列答案
相关题目
