题目内容
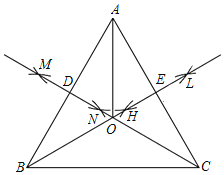
【题目】如图,![]() ABC中,AB=AC,AD⊥BC于点D,延长AB至点E,使∠AEC=∠DAB.判断CE与AD的数量关系,并证明你的结论.
ABC中,AB=AC,AD⊥BC于点D,延长AB至点E,使∠AEC=∠DAB.判断CE与AD的数量关系,并证明你的结论.
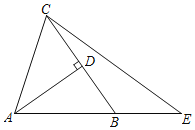
【答案】CE=2AD,证明详见解析
【解析】
延长AD至点N使DN=AD,AN交CE于点M,连接CN,根据等腰三角形的性质得到MA=ME,根据全等三角形的性质得到∠N=∠DAB.根据平行线的性质得到∠3=∠AEC.求得MC=MN,于是得到结论.
解:CE=2AD;
理由:延长AD至点N使DN=AD,AN交CE于点M,连接CN,
∵∠DAB=∠AEC,
∴MA=ME,
∵AB=AC,AD⊥BC,
∴∠CAD=∠DAB,BD=CD,∠1=∠2=90°.
∴![]() ABD≌
ABD≌![]() NCD(AAS),
NCD(AAS),
∴∠N=∠DAB.
∴CN∥AE.
∴∠3=∠AEC.
∴∠3=∠N.
∴MC=MN,
∴CE=MC+ME
=MN+MA
=AN
=2AD.

练习册系列答案
相关题目
【题目】生活与数学
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | 5 | 6 | |
7 | 8 | 9 | 10 | 11 | 12 | 13 |
14 | 15 | 16 | 17 | 18 | 19 | 20 |
21 | 22 | 23 | 24 | 25 | 26 | 27 |
(1)姆同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是48,那么这四个数是_______.
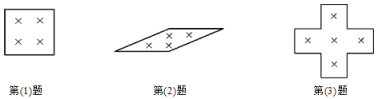
(2)丽也在上面的日历上圈出2×2个数,斜框内的四个数的和是46,则它们分别是_____.
(3)莉也在日历上圈出5个数,呈十字框形,它们的和是55,则中间的数是______.
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是______号?