题目内容
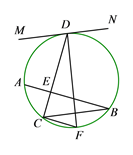
【题目】如图,圆中的弦AB与弦CD垂直于点E,点F在![]() 上,
上, ![]() ,直线MN过点D,且∠MDC=∠DFC,求证:直线MN是该圆的切线.
,直线MN过点D,且∠MDC=∠DFC,求证:直线MN是该圆的切线.
【答案】详见解析.
【解析】试题分析:利用同弧所对的圆周角相等的出∠ABC=∠BCF,再由平行线额判定与性质求出∠DCF=90°,由等量代换求出∠MDC+∠CDF=90°,即可求出结论.
证明:设该圆的圆心为点O,
在⊙O中,∵ ![]() =
=![]() ,
,
∴ ∠AOC=∠BOF.

又 ∠AOC=2∠ABC,∠BOF=2∠BCF,
∴ ∠ABC=∠BCF.
∴ AB∥CF.
∴ ∠DCF=∠DEB.
∵ DC⊥AB,
∴ ∠DEB=90°.
∴ ∠DCF=90°.
∴ DF为⊙O直径.
且 ∠CDF+∠DFC=90°.
∵ ∠MDC=∠DFC,
∴ ∠MDC+∠CDF=90°.
即 DF⊥MN.
又∵ MN过点D,
∴ 直线MN是⊙O的切线 .

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
【题目】生活与数学
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | 5 | 6 | |
7 | 8 | 9 | 10 | 11 | 12 | 13 |
14 | 15 | 16 | 17 | 18 | 19 | 20 |
21 | 22 | 23 | 24 | 25 | 26 | 27 |
(1)姆同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是48,那么这四个数是_______.
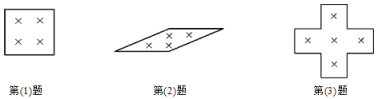
(2)丽也在上面的日历上圈出2×2个数,斜框内的四个数的和是46,则它们分别是_____.
(3)莉也在日历上圈出5个数,呈十字框形,它们的和是55,则中间的数是______.
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是______号?