题目内容
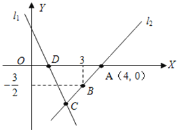
【题目】定义:如点M、N把线段AB分割成AM、MN、BN,若以AM、MN、BN,为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.
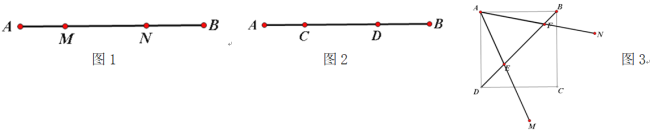
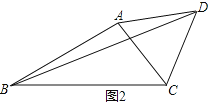
(1)如图2,已知点C、D是线段AB的勾股分割点,若AC=3,DB=4,求CD的长;
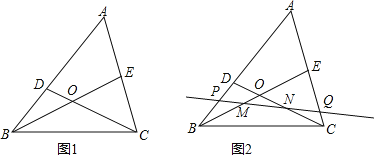
(2)如图3,在正方形ABCD中,∠MAM=45°,角的两边AM、AN分别交BD于E、F(不与端点重合),求证:E、F是BD的勾股分割点.
【答案】(1)5或![]() .(2)证明过程见解析.
.(2)证明过程见解析.
【解析】
(1)①当CD为最大线段时,由勾股定理求出CD的长;②当BD为最大线段时,由勾股定理求出CD即可;
(2)将△ABF绕点A顺时针旋转90°得到△ADH,连接HE,只要证明△EAH≌△EAF,推出EF=HE,再证明∠HDE=90°即可.
(1)解:①当CD为最大线段时,
∵点C、D是线段AB的勾股分割点
∴CD=![]() =
=![]() =5
=5
②当BD为最大线段时,
∵点C、D是线段AB的勾股分割点
∴CD=![]() =
=![]() =
=![]()
综上,CD的长为5或![]() .
.
(2)证明:如图,将△ABF绕点A顺时针旋转90°得到△ADH,连接HE

∵∠BAF+∠DAE=90°-∠MAN=90°-45°=45°,∠BAF=∠DAH
∴∠DAH+∠DAE=45°
即∠EAH=45°
在△EAH和△EAF中

∴△EAH≌△EAF(SAS)
∴EH=EF
∵四边形ABCD为正方形,BD为对角线
∴∠ABF=∠ADB=45°
∴∠ADH=∠ABF=∠ADB =45°
∴∠HDE=90°
在Rt△DHE中,HE2=DH2+DE2
∵DH=BF,EF=HE
∴EF2=BF2+DE2
∴E、F是BD的勾股分割点.

【题目】生活与数学
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | 5 | 6 | |
7 | 8 | 9 | 10 | 11 | 12 | 13 |
14 | 15 | 16 | 17 | 18 | 19 | 20 |
21 | 22 | 23 | 24 | 25 | 26 | 27 |
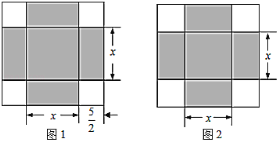
(1)姆同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是48,那么这四个数是_______.
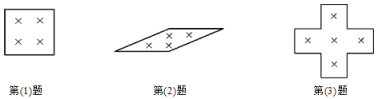
(2)丽也在上面的日历上圈出2×2个数,斜框内的四个数的和是46,则它们分别是_____.
(3)莉也在日历上圈出5个数,呈十字框形,它们的和是55,则中间的数是______.
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是______号?