题目内容
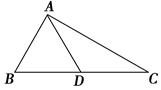
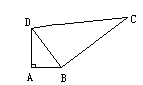
如图,在△ABD中,∠A是直角,AB=3,AD=4,BC=12,DC=13,求四边形ABCD的面积。

36.
试题分析:根据勾股定理求得BD=5;由勾股定理的逆定理判定△BCD为直角三角形,则四边形ABCD的面积=△ABD的面积+△BCD的面积.
试题解析:∵在△ABD中,∠A是直角,AB=3,AD=4,
∴由勾股定理得 BD2=AD2+AB2=25.则BD=5,
又∵在△BCD中,BC=12,DC=13,
∴CD2=BD2+BC2=169,
∴△BCD为直角三角形,且∠DBC=90°,
∴S四边形ABCD=S△ABD+S△BCD=
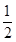 AD•AB+
AD•AB+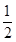 BD•BC=
BD•BC=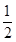 ×4×3+
×4×3+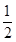 ×5×12=36.
×5×12=36.即四边形ABCD的面积是36.
考点: 1.勾股定理;2.勾股定理的逆定理.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
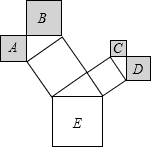
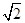
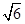
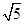
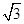
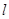 上有三个正方形
上有三个正方形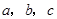 ,若
,若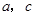 的面积分别为5和11, 则
的面积分别为5和11, 则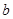 的面积为( )
的面积为( )