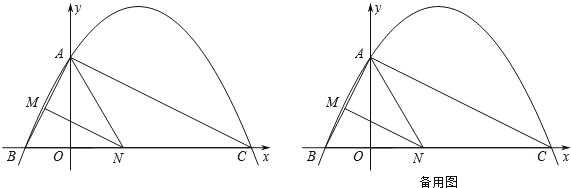
��Ŀ����
����Ŀ����ͼ����֪���κ��� y��ax2+![]() x+c ��ͼ���� y �ύ�ڵ� A��0��4����
x+c ��ͼ���� y �ύ�ڵ� A��0��4����
�� x �ύ�ڵ� B��C���� C ����Ϊ��8��0�������� AB��AC��
��1����ֱ��д�����κ��� y��ax2+![]() x+c �ı���ʽ��
x+c �ı���ʽ��
��2���ж���ABC ����״����˵�����ɣ�
��3������ N �� x �����˶������Ե� A��N��C Ϊ������������ǵ���������ʱ�� ��ֱ��д����ʱ�� N �����ꣻ
��4������ N ���߶� BC ���˶�������� B��C �غ��������� N �� NM��AC����AB �ڵ� M������AMN ������ʱ�����ʱ�� N �����꣮
���𰸡���1��y����![]() x2+
x2+![]() x+4����2����ABC��ֱ�������Σ����ɼ���������3����N������ֱ�Ϊ����8��0������8��4
x+4����2����ABC��ֱ�������Σ����ɼ���������3����N������ֱ�Ϊ����8��0������8��4![]() ��0������3��0������8+4
��0������3��0������8+4![]() ��0������4������AMN������ʱ��N������Ϊ��3��0����
��0������4������AMN������ʱ��N������Ϊ��3��0����
��������
��1�����ô���ϵ������⼴�ɣ�
��2�������AB��AC��BC�ij���Ȼ����ݹ��ɶ������涨������֤�á�ABCΪֱ����������
��3���ֱ���A��C����ΪԲ�ģ�AC��Ϊ�뾶��������x�ύ�������㣬��AC�Ĵ�ֱƽ������x�ύ��һ���㣬�ֱ���õ�N�����꼴�ɣ�
��4�����N������Ϊ��n��0������BN��n+2����M����MD��x���ڵ�D���������������ƶ�Ӧ�߳ɱ������MD��![]() ��n+2����Ȼ�����S��AMN��S��ABN��S��BMN�ó�����n�Ķ��κ��������ݺ�������ʽ��ü���.
��n+2����Ȼ�����S��AMN��S��ABN��S��BMN�ó�����n�Ķ��κ��������ݺ�������ʽ��ü���.
������1�������κ���y��ax2+![]() x+c��ͼ����y�ύ�ڵ�A��0��4������x�ύ�ڵ�B��C����C����Ϊ��8��0����
x+c��ͼ����y�ύ�ڵ�A��0��4������x�ύ�ڵ�B��C����C����Ϊ��8��0����
![]() ��
��
���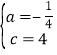 ��
��
�������߱���ʽ��y����![]() x2+
x2+![]() x+4��
x+4��
��2����ABC��ֱ�������Σ�
�� y��0������![]() x2+
x2+![]() x+4��0�� ��� x1��8��x2����2��
x+4��0�� ��� x1��8��x2����2��
���� B ����������2��0����
����֪�ɵã�
��Rt�� ABO����AB2��BO2+AO2��22+42��20��
��Rt��AOC����AC2��AO2+CO2��42+82��80��
����BC��OB+OC��2+8��10��
������ABC����AB2+AC2��20+80��102��BC2��
���ABC ��ֱ����������
��3����A��0��4����C��8��0����
��AC��![]() ��4
��4![]() ��
��
����AΪԲ�ģ���AC��Ϊ�뾶��Բ���� x ���� N����ʱ N ������Ϊ����8��0����
����CΪԲ������AC��Ϊ�뾶��Բ����x����N����ʱN������Ϊ��8��4![]() ��0����8+4
��0����8+4 ![]() ��0����
��0����
����AC�Ĵ�ֱƽ���ߣ���x����N����ʱN������Ϊ��3��0����
���ϣ�����N��x�����˶������Ե�A��N��CΪ������������ǵ���������ʱ�� ��N������ֱ�Ϊ����8��0������8��4![]() ��0������3��0������8+4
��0������3��0������8+4![]() ��0����
��0����
��4�����N������Ϊ��n��0������BN��n+2����M����MD��x���ڵ�D��
��MD��OA��
���BMD�ס�BAO��
��![]() ��
��
��MN��AC��
��![]() ��
��
��![]() ��
��
��AO��4��BC��10��BN��n+2��
��MD��![]() ��n+2����
��n+2����
��S��AMN��S��ABN��S��BMN��
��![]() BNOA��
BNOA��![]() BNMD
BNMD
��![]() ��n+2����4��
��n+2����4��![]() ��
��![]() ��n+2��2
��n+2��2
����![]() ��n��3��2+5��
��n��3��2+5��
������AMN ������ʱ��N������Ϊ��3��0����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�