Question

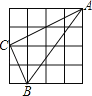
【题目】正方形ABCD,点E为AB的中点,且BF=BC.

（1）如图1，求证：DE⊥EF.

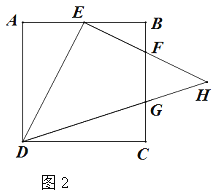
（2）如图2，若点G在BC上，且CD=3CG，DG、EF交于H点，求的值.

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）连接DF，设BF=a，利用勾股定理用a表示出DE、EF、DF的长，然后根据勾股定理的逆定理即可得出结论；

（2）连接EG，延长BC至M，使CM＝AE，连接DM，可得△DAE≌△DCM，得出DE=DM，∠ADE=∠CDM，推出∠EDM=90°，然后利用勾股定理分别用a表示EG和MG，证出EG=MG，利用SSS可证得△DGE≌△DGM，进而证得∠EDH=45°，利用勾股定理求出DH，即可得出的值．

（1）连接DF，设BF=a，则CF=3a，AD=CD=4a，AE=BE=2a，

由勾股定理得：DF=5a，DE= 2a，EF=a，

∴DE2+EF2=( 2a)2+(a)2=25a2，DF2=25a2，

∴DE2+EF2=DF2，

∴∠DEF=90，

∴DE⊥EF；

（2）连接EG，延长BC至M，使CM＝AE，连接DM，

在△DAE和△DCM中，

，

∴△DAE≌△DCM(SAS)，

∴DE=DM，∠ADE=∠CDM，

∴∠EDM=∠ADC=90°，

∵CD=3CG，

∴CG=a，

∴MG=MC+CG=2a+a=a，

在RtΔBEG中，由勾股定理得：EG=a，

∴EG=MG，

∴△DGE≌△DGM（SSS），

∴∠EDG=∠MDG=45°，

∴△EDH是等腰直角三角形，

∴DH=DE=EH，

∴=．