Question

【题目】已知函数与，当满足时，两个函数的图象存在个公共点，则满足的条件是( )

A.B.C.D.

Answer 1

【答案】D

【解析】

求出函数y=（k-1）x+2k-1的图象过定点A（-2，1），画出y=|x-1|的图象，求出两个函数的图象存在个公共点时k的临界值即可．

解：由已知，当x=-2时，y=-2（k-1）+2k-1=1，
∴函数y=（k-1）x+2k-1的图象过定点A（-2，1）
如图：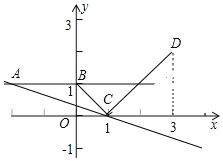

y=|x-1|的图象如图为折线BCD，其中点B（0，1），C（1，0），D（3，2）
当函数y=（k-1）x+2k-1的图象过点C（1，0）时，与折线BCD恰好有一个交点，
此时，k=；
当直线过点A、B时，AB∥x轴，直线AB与折线BCD有两个交点
此时，k-1=0，即k=1；

∴满足的条件是.

故选：D.