题目内容
【题目】如图,ABCD中,E、F为对角线AC上的点,且AE=CF,试探索四边形DEBF的形状并说明你的理由.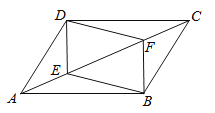
【答案】证明:四边形DEBF是平行四边形
∵ABCD是平行四边形,
∴AD=BC,AD∥BC
∴∠DAF=∠BCA,
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
在△ADF与△CBE中,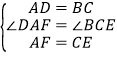 ,
,
∴△ADF≌△CBE(SAS),
∴∠DFA=∠BEC,DF=BE,
∴DF∥BE,
∴四边形DEBF是平行四边形.
【解析】根据平行四边形的性质对边平行且相等得到AD与BC平行且相等,由AD与BC平行得到内错角∠DAF与∠BCE相等,再由已知的AE=CF,根据“SAS”得到△ADF与△CBE全等,根据全等三角形的性质得到DF与EB相等且∠DFA与∠BEC相等,由内错角相等两直线平行得到DF与BE平行,根据一组对边平行且相等的四边形为平行四边形即可得到四边形DEBF的形状.
【考点精析】解答此题的关键在于理解平行四边形的判定与性质的相关知识,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.

【题目】2016年4月30日至5月2日,河北省共接待游客1708.3万人次,实现旅游收入106.5亿元,旅行社的小王想了解某企业员工个人的旅游年消费情况,他随机抽取部分员工进行调查,并将统计结果绘制成如表所示的频数分布表,则下列说法中不正确的是( )
个人旅游年消费金额x/元 | x≤2000 | 2000<x≤4000 | 4000<x≤6000 | 6000<x≤8000 | 8000<x≤10000 |
频数 | 12 | 25 | 31 | 22 | 10 |
A.小王随机抽取了100名员工
B.在频数分布表中,组距是2000,组数是5组
C.个人旅游年消费金额在6000元以上的人数占随机抽取人数的22%
D.在随机抽取的员工中,个人旅游年消费金额在4000元以下的共有37人
