Question

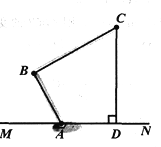
【题目】一货轮在A处测得灯塔P在货轮的北偏西23°的方向上，随后货轮以80海里/时的速度按北偏东30°的方向航行，1小时后到达B处，此时又测得灯塔P在货轮的北偏西68°的方向上，求此时货轮距灯塔P的距离PB.（参考数据：，，）

Answer 1

【答案】（海里）

【解析】

过B做BC⊥AP与C点,可得∠A=23+30=53，∠ABC=90-53=37，∠PBC=45，易得AB=80海里,可得BC的长、PB的长

解：如图

过B做BC⊥AP与C点，由题意得：∠A=23+30=53，

AB=180=80,∠PBM=68,∠ABN=30

∠ABC=90-53=37,

∠PBC=180-∠PBM-∠ABN-∠ABC=180-68-37-30=45,

在△ABC中，∠ABC=37，∠BCA=90，

sinA===,BC=64,

在△PBC中, ∠BCP=90,

cos∠CBP===,

BP=（海里）

答:此时货轮距灯塔P的距离PB为海里.