题目内容
【题目】如图，某公园内有座桥，桥的高度是5米，CB⊥DB，坡面AC的倾斜角为45°，为方便老人过桥，市政部门决定降低坡度，使新坡面DC的坡度为i= 
：3．若新坡角外需留下2米宽的人行道，问离原坡角（A点处）6米的一棵树是否需要移栽？（参考数据： 
≈1.414， ≈1.732）
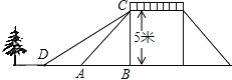
【答案】不需要移栽，理由见解析
【解析】
根据题意得到三角形ABC为等腰直角三角形，求出AB的长，在直角三角形BCD中，根据新坡面的坡度求出∠BDC的度数为30，利用30度角所对的直角边等于斜边的一半求出DC的长，再利用勾股定理求出DB的长，由DB-AB求出AD的长，然后将AD+2与6进行比较，若大于则需要移栽，反之不需要移栽．
解：不需要移栽，理由为： ∵CB⊥AB，∠CAB=45°，
∴△ABC为等腰直角三角形，
∴AB=BC=5米，
在Rt△BCD中，新坡面DC的坡度为i= 
：3，即∠CDB=30°，
∴DC=2BC=10米，BD= BC=5 米，
∴AD=BD﹣AB=（5 ﹣5）米≈3.66米，
∵2+3.66=5.66＜6，
∴不需要移栽．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
【题目】阳光市场某个体商户购进某种电子产品，每个进价是50元.调查发现，当售价是80元时，平均一周可卖出160个，而当售价每降低2元时，平均一周可多卖出20个.若设每个电子产品降价x元，
（1）根据题意，填表：
进价（元） | 售价（元） | 每件利润（元） | 销量（个） | 一周总利润（元） | |
降价前 | 50 | 80 | 30 | 160 |
|
降价后 | 50 |
（2）若商户计划每周盈利5200元，且尽量减少库存，则应降价多少元？
