Question

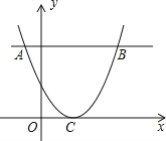
【题目】如图，抛物线y=2（x-2）2与平行于x轴的直线交于点A，B，抛物线顶点为C，△ABC为等边三角形，求S△ABC．

Answer 1

【答案】

【解析】

过B作BP⊥x轴交于点P，连接AC，BC，由抛物线y=得C（2，0），

于是得到对称轴为直线x=2，设B（m，n），根据△ABC是等边三角形，得到BC=AB=2m-4，∠BCP=∠ABC=60°，求出PB=PC=（m-2），由于PB=n=，于是得到

（m-2）=，解方程得到m的值，然后根据三角形的面积公式即可得到结果．

解：过B作BP⊥x轴交于点P，连接AC，BC，

由抛物线y=得C（2，0），

∴对称轴为直线x=2，

设B（m，n），

∴CP=m-2，

∵AB∥x轴，

∴AB=2m-4，

∵△ABC是等边三角形，

∴BC=AB=2m-4，∠BCP=∠ABC=60°，

∴PB=PC=（m-2），

∵PB=n=，

∴（m-2）=，

解得m=，m=2（不合题意，舍去），

∴AB=，BP=，

∴S△ABC=．