题目内容
【题目】公司有345台电脑需要一次性运送到某学校,计划租用甲、乙两种货车共8辆已知每辆甲种货车一次最多运送电脑45台、租车费用为400元,每辆乙种货车一次最多运送电脑30台、租车费用为280元
(Ⅰ)设租用甲种货车![]() 辆(
辆(![]() 为非负整数),试填写下表.
为非负整数),试填写下表.
表一:
租用甲种货车的数量/辆 | 3 | 7 |
|
租用的甲种货车最多运送电脑的数量/台 | 135 | ||
租用的乙种货车最多运送电脑的数量/台 | 150 |
表二:
租用甲种货车的数量/辆 | 3 | 7 |
|
租用甲种货车的费用/元 | 2800 | ||
租用乙种货车的费用/元 | 280 |
(Ⅱ)给出能完成此项运送任务的最节省费用的租车方案,并说明理由
【答案】(Ⅰ)表一:![]() ,
,![]() ,
,![]() ,
,![]() ,表二:
,表二:![]() ,
,![]() ,
,![]()
![]() ;(Ⅱ)能完成此项运送任务的最节省费用的租车方案为甲种货车7辆、乙种货车1辆,见解析.
;(Ⅱ)能完成此项运送任务的最节省费用的租车方案为甲种货车7辆、乙种货车1辆,见解析.
【解析】
(Ⅰ)根据计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元,可以分别把表一和表二补充完整;
(Ⅱ)设租用甲种货车![]() 辆时,两种货车的总费用为y元;根据(Ⅰ)中的数据和y=租用甲车的费用+租用乙车的费用,得出y与x的函数关系式,利用函数的增减性即可得出.
辆时,两种货车的总费用为y元;根据(Ⅰ)中的数据和y=租用甲车的费用+租用乙车的费用,得出y与x的函数关系式,利用函数的增减性即可得出.
解:(Ⅰ)由题意可得,
在表一中,当甲车7辆时,运送的机器数量为:45×7=315(台),则乙车8-7=1辆,运送的机器数量为:30×1=30(台),
当甲车x辆时,运送的机器数量为:45×x=45x(台),则乙车(8-x)辆,运送的机器数量为:30×(8-x)=-30x+240(台),
在表二中,当租用甲货车3辆时,租用甲种货车的费用为:400×3=1200(元),则租用乙种货车8-3=5辆,租用乙种货车的费用为:280×5=1400(元),
当租用甲货车x辆时,租用甲种货车的费用为:400×x=400x(元),则租用乙种货车(8-x)辆,租用乙种货车的费用为:280×(8-x)=-280x+2240(元),
故答案为:表一:315,45x,30,-30x+240;
表二:1200,400x,1400,-280x+2240;
(Ⅱ)能完成此项运送任务的最节省费用的租车方案是甲车7辆,乙车1辆,
理由如下:设租用甲种货车![]() 辆时,两种货车的总费用为y元;
辆时,两种货车的总费用为y元;
∴![]() ,
,
∵![]() ,解得
,解得![]() .
.
∵![]() ,
,
∴![]() 随
随![]() 的增大而增大
的增大而增大
∴当![]() 时,
时,![]() 取得最小值,此时8-x=1
取得最小值,此时8-x=1
答:能完成此项运送任务的最节省费用的租车方案为甲种货车7辆、乙种货车1辆.

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案【题目】(某中学九年级学生共600人,其中男生320人,女生280人.该校对九年级所有学生进行了一次体育模拟测试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成如下的统计表:
类别 | 成绩(分) | 频数 | 频率 |
I | 40 | 36 | 0.3 |
II | 37—39 | a | b |
III | 34—36 | 24 | 0.2 |
IV | 31—33 | 6 | 0.05 |
合计 | c | 1 | |
(1)a= ; b= ;
(2)若将该表绘制成扇形统计图,那么Ⅲ类所对应的圆心角是 °;
(3)若随机抽取的学生中有64名男生和56名女生,请解释“随机抽取64名男生和56名女生”的合理性;
(4)估计该校九年级学生体育测试成绩是40分的人数.
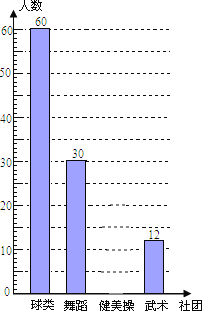
【题目】为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
社团类别 | 人数 | 占总人数比例 |
球类 | 60 | m |
舞蹈 | 30 | 0.25 |
健美操 | n | 0.15 |
武术 | 12 | 0.1 |
(1)求样本容量及表格中m、n的值;
(2)请补全统计图;
(3)被调查的60个喜欢球类同学中有3人最喜欢足球,若该校有3000名学生,请估计该校最喜欢足球的人数.