题目内容
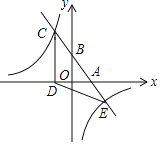
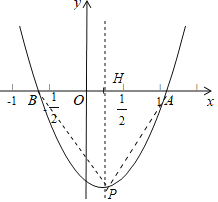
【题目】如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)与x轴交于A,B两点,顶点P(m,n).给出下列结论:①2a+c<0;②若(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(
,y2),(![]() ,y3)在抛物线上,则y1>y2>y3;③关于x的方程ax2+bx+k=0有实数解,则k>c﹣n;④当n=﹣
,y3)在抛物线上,则y1>y2>y3;③关于x的方程ax2+bx+k=0有实数解,则k>c﹣n;④当n=﹣![]() 时,△ABP为等腰直角三角形.其中正确结论是______(填写序号).
时,△ABP为等腰直角三角形.其中正确结论是______(填写序号).

【答案】②④
【解析】
利用二次函数的对称轴、顶点坐标、增减性、与坐标轴的交点等性质一一判断即可.
∵-![]() <
<![]() ,a>0,
,a>0,
∴a>-b,
∵x=-1时,y>0,
∴a-b+c>0,
∴2a+c>a-b+c>0,故①错误,
若(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(
,y2),(![]() ,y3)在抛物线上,
,y3)在抛物线上,
由图象法可知,y1>y2>y3;故②正确,
∵抛物线与直线y=t有交点时,方程ax2+bx+c=t有解,t≥n,
∴ax2+bx+c-t=0有实数解
要使得ax2+bx+k=0有实数解,则k=c-t≤c-n;故③错误,
设抛物线的对称轴交x轴于H.
∵![]() ,
,
∴b2-4ac=4,
∴x=![]() ,
,
∴|x1-x2|=![]() ,
,
∴AB=2PH,
∵BH=AH,
∴PH=BH=AH,
∴△PAB是直角三角形,
∵PA=PB,
∴△PAB是等腰直角三角形.故④正确.
故答案为②④.

 名校课堂系列答案
名校课堂系列答案【题目】公司有345台电脑需要一次性运送到某学校,计划租用甲、乙两种货车共8辆已知每辆甲种货车一次最多运送电脑45台、租车费用为400元,每辆乙种货车一次最多运送电脑30台、租车费用为280元
(Ⅰ)设租用甲种货车![]() 辆(
辆(![]() 为非负整数),试填写下表.
为非负整数),试填写下表.
表一:
租用甲种货车的数量/辆 | 3 | 7 |
|
租用的甲种货车最多运送电脑的数量/台 | 135 | ||
租用的乙种货车最多运送电脑的数量/台 | 150 |
表二:
租用甲种货车的数量/辆 | 3 | 7 |
|
租用甲种货车的费用/元 | 2800 | ||
租用乙种货车的费用/元 | 280 |
(Ⅱ)给出能完成此项运送任务的最节省费用的租车方案,并说明理由