题目内容
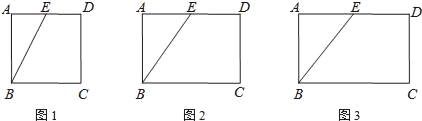
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,若
的中点,若![]() 为
为![]() 边上的两个动点,且
边上的两个动点,且![]() ,若想使得四边形
,若想使得四边形![]() 的周长最小,则
的周长最小,则![]() 的长度应为__________.
的长度应为__________.

【答案】![]()
【解析】
要使四边形APQE的周长最小,由于AE与PQ都是定值,只需AP+EQ的值最小即可.为此,先在BC边上确定点P、Q的位置,可在AD上截取线段AF=DE=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,则此时AP+EQ=EG最小,然后过G点作BC的平行线交DC的延长线于H点,证![]() 即可.
即可.
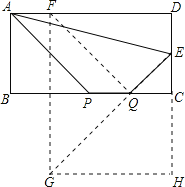
解:如图,在AD上截取线段AF=DE=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,过G点作BC的平行线交DC的延长线于H点.
∵E为CD的中点,∴CE=2
∴GH=DF=5,EH=2+4=6,∠H=90°,
∵BC//GH
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴CQ=![]() ,
,
∴BP=CB-PQ-CQ=7-2-![]() .
.
故答案为:![]() .
.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
【题目】公司有345台电脑需要一次性运送到某学校,计划租用甲、乙两种货车共8辆已知每辆甲种货车一次最多运送电脑45台、租车费用为400元,每辆乙种货车一次最多运送电脑30台、租车费用为280元
(Ⅰ)设租用甲种货车![]() 辆(
辆(![]() 为非负整数),试填写下表.
为非负整数),试填写下表.
表一:
租用甲种货车的数量/辆 | 3 | 7 |
|
租用的甲种货车最多运送电脑的数量/台 | 135 | ||
租用的乙种货车最多运送电脑的数量/台 | 150 |
表二:
租用甲种货车的数量/辆 | 3 | 7 |
|
租用甲种货车的费用/元 | 2800 | ||
租用乙种货车的费用/元 | 280 |
(Ⅱ)给出能完成此项运送任务的最节省费用的租车方案,并说明理由