题目内容
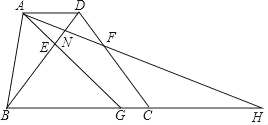
【题目】如图,矩形ABCD中,AB=4,AD=6,E为射线BC上一动点(不与C重合),△CDE的外接圆交AE于P,若CP=CD,则AP的值为_____.

【答案】![]()
【解析】
连接PD,如图,利用圆周角定理证明∠EPD=90°,∠CDP=∠CED,再证明∠AEB=∠CED,则可判断△ABE≌△DCE,所以BE=CE=![]() BC=3,再利用勾股定理计算出AE,然后证明Rt△ADP∽Rt△EAB,从而利用相似比可计算出AP的长.
BC=3,再利用勾股定理计算出AE,然后证明Rt△ADP∽Rt△EAB,从而利用相似比可计算出AP的长.
连接PD,如图,
∵∠ECD=90°,
∴DE为直径
∴∠EPD=90°,
∵CP=CD,
∴∠CDP=∠CED,
∵∠AEB=∠CDP,
∴∠AEB=∠CED,
∵AB=CD,∠B=∠ECD,
∴△ABE≌△DCE,
∴BE=CE=![]() BC=3,
BC=3,
在Rt△ABE中,AE=![]() =5,
=5,
∵AD∥BC,
∴∠BEA=∠DAE,
∴Rt△ADP∽Rt△EAB,
∴![]() ,即
,即![]() ,
,
∴AP=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目