题目内容
【题目】如图,在△ABC中,AB=AC=2![]() ,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为_____.
,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为_____.

【答案】3![]() ﹣3.
﹣3.
【解析】
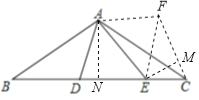
将△ABD绕点A逆时针旋转120°得到△ACF,连接EF,过点E作EM⊥CF于点M,过点A作AN⊥BC于点N,由AB=AC=2![]() 、∠BAC=120°,可得出BC=6、∠B=∠ACB=30°,通过角的计算可得出∠FAE=60°,结合旋转的性质可证出△ADE≌△AFE(SAS),进而可得出DE=FE,设CE=2x,则CM=x,EM=
、∠BAC=120°,可得出BC=6、∠B=∠ACB=30°,通过角的计算可得出∠FAE=60°,结合旋转的性质可证出△ADE≌△AFE(SAS),进而可得出DE=FE,设CE=2x,则CM=x,EM=![]() x、FM=4x-x=3x、EF=ED=6-6x,在Rt△EFM中利用勾股定理可得出关于x的一元二次方程,解之可得出x的值,再将其代入DE=6-6x中即可求出DE的长.
x、FM=4x-x=3x、EF=ED=6-6x,在Rt△EFM中利用勾股定理可得出关于x的一元二次方程,解之可得出x的值,再将其代入DE=6-6x中即可求出DE的长.
将△ABD绕点A逆时针旋转120°得到△ACF,连接EF,过点E作EM⊥CF于点M,过点A作AN⊥BC于点N,如图所示,
 ,
,
∵AB=AC=2![]() ,∠BAC=120°,
,∠BAC=120°,
∴BN=CN,∠B=∠ACB=30°,
在Rt△BAN中,∠B=30°,AB=2![]() ,
,
∴AN=![]() AB=
AB=![]() ,BN=
,BN=![]() =3,
=3,
∴BC=6,
∵∠BAC=12°,∠DAE=60°,
∴∠BAD+∠CAE=60°,
∴∠FAE=∠FAC+∠CAE=∠BAD+∠CAE=60°,
在△ADE和△AFE中, ,
,
∴△ADE≌△AFE(SAS),
∴DE=FE,
∵BD=2CE,BD=CF,∠ACF=∠B=30°,
∴设CE=2x,则CM=x,EM=![]() x,FM=4xx=3x,EF=ED=66x.
x,FM=4xx=3x,EF=ED=66x.
在Rt△EFM中,FE=66x,FM=3x,EM=![]() x,
x,
∴EF2=FM2+EM2,,即(66x)2=(3x)2+(![]() x)2,
x)2,
解得:x1=![]() ,x2=
,x2=![]() (不合题意,舍去),
(不合题意,舍去),
∴DE=66x=![]() .
.
故答案为:![]() .
.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目