题目内容
【题目】如图,⊙O与∠α的两边相切,若∠α=60°,则图中阴影部分的面积S关于⊙O的半径r的函数图象大致是( )
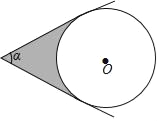
A. 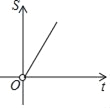 B.
B. 
C. 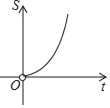 D.
D. 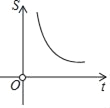
【答案】C
【解析】
过O点作两切线的垂线,垂足分别为A、B,连接OP,如图,利用切线的性质得OA=OB=r,根据切线长定理得到∠APO=∠BPO=30°,则AP![]() OA
OA![]() r,再利用四边形内角和计算出∠AOB=120°,接着利用扇形面积公式得到S=(
r,再利用四边形内角和计算出∠AOB=120°,接着利用扇形面积公式得到S=(![]() π)r2(r>0),然后根据解析式对各选项进行判断.
π)r2(r>0),然后根据解析式对各选项进行判断.
过O点作两切线的垂线,垂足分别为A、B,连接OP,如图,则OA=OB=r,∠APO=∠BPO=30°,∴AP![]() OA
OA![]() r.
r.
∵∠OAP=∠OBP=90°,∴∠AOB=180°﹣α=180°﹣60°=120°,∴S=S四边形AOBP﹣S扇形AOB=2![]() r
r![]() =(
=(![]() π)r2(r>0).
π)r2(r>0).
故选C.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目