题目内容
【题目】点P是矩形ABCD对角线AC所在直线上的一个动点(点P不与点A,C重合),分别过点A,C向直线BP作垂线,垂足分别为点E,F,点O为AC的中点.

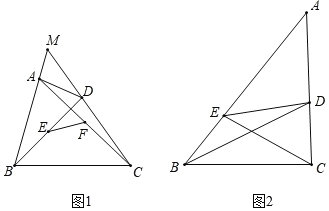
(1)如图1,当点P与点O重合时,请你判断OE与OF的数量关系;
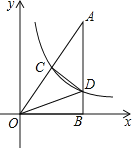
(2)当点P运动到如图2所示位置时,请你在图2中补全图形并通过证明判断(1)中的结论是否仍然成立;
(3)若点P在射线OA上运动,恰好使得∠OEF=30°时,猜想此时线段CF,AE,OE之间有怎样的数量关系,直接写出结论不必证明.
【答案】(1)OE=OF.理由见解析;(2)补全图形如图所示见解析,OE=OF仍然成立;(3)CF=OE+AE或CF=OE﹣AE.
【解析】
(1)根据矩形的性质以及垂线,即可判定![]() ,得出OE=OF;
,得出OE=OF;
(2)先延长EO交CF于点G,通过判定![]() ,得出OG=OE,再根据
,得出OG=OE,再根据![]() 中,
中,![]() ,即可得到OE=OF;
,即可得到OE=OF;
(3)根据点P在射线OA上运动,需要分两种情况进行讨论:当点P在线段OA上时,当点P在线段OA延长线上时,分别根据全等三角形的性质以及线段的和差关系进行推导计算即可.
(1)OE=OF.理由如下:
如图1.
∵四边形ABCD是矩形,∴ OA=OC.
∵![]() ,
,![]() ,∴
,∴![]() .
.
∵在![]() 和
和![]() 中,
中, ,∴
,∴![]() ,∴ OE=OF;
,∴ OE=OF;
(2)补全图形如图2,OE=OF仍然成立.证明如下:
延长EO交CF于点G.
∵![]() ,
,![]() ,∴ AE//CF,∴
,∴ AE//CF,∴![]() .
.
又∵点O为AC的中点,∴ AO=CO.
在![]() 和
和![]() 中,
中,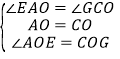 ,∴
,∴![]() ,∴ OG=OE,∴
,∴ OG=OE,∴![]() 中,
中,![]() ,∴ OE=OF;
,∴ OE=OF;
(3)CF=OE+AE或CF=OE-AE.
证明如下:①如图2,当点P在线段OA上时.
∵![]() ,
,![]() ,∴
,∴![]() ,由(2)可得:OF=OG,∴
,由(2)可得:OF=OG,∴![]() 是等边三角形,∴ FG=OF=OE,由(2)可得:
是等边三角形,∴ FG=OF=OE,由(2)可得:![]() ,∴ CG=AE.
,∴ CG=AE.
又∵ CF=GF+CG,∴ CF=OE+AE;
②如图3,当点P在线段OA延长线上时.
∵![]() ,
,![]() ,∴
,∴![]() ,同理可得:
,同理可得:![]() 是等边三角形,∴ FG=OF=OE,同理可得:
是等边三角形,∴ FG=OF=OE,同理可得:![]() ,∴ CG=AE.
,∴ CG=AE.
又∵ CF=GF-CG,∴ CF=OE-AE.


 字词句段篇系列答案
字词句段篇系列答案