题目内容
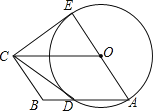
【题目】已知:如图,![]() 、
、![]() 都是等腰三角形,且
都是等腰三角形,且![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,点
,点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.以下
的中点.以下![]() 个结论:①
个结论:①![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④连
是等边三角形;④连![]() ,则
,则![]() 平分
平分![]() .正确的是( )
.正确的是( )
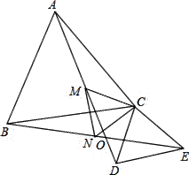
A.①②③B.①②④C.①③④D.①②③④
【答案】B
【解析】
①根据∠ACB=∠DCE求出∠ACD=∠BCE,证出![]() 即可得出结论,故可判断;
即可得出结论,故可判断;
②根据全等求出∠CAD=∠CBE,根据三角形外角定理得∠DOB=∠OBA+∠BAO,通过等角代换能够得到∠DOB=∠CBA+∠BAC,根据三角形内角和定理即可求出∠CBA+∠BAC,即可求出∠DOB,故可判断;
③根据已知条件可求出AM=BN,根据SAS可求出![]() ,推出CM=CN,∠ACM=∠BCN,然后可求出∠MCN=∠ACB=α,故可判断
,推出CM=CN,∠ACM=∠BCN,然后可求出∠MCN=∠ACB=α,故可判断![]() 的形状;
的形状;
④在AD上取一点P使得DP=EO,连接CP,根据![]() ,可求出∠CEO=∠CDP,根据SAS可求出
,可求出∠CEO=∠CDP,根据SAS可求出 ![]() ,可得∠COE=∠CPD,CP=CO,进而得到 ∠COP=∠COE,故可判断.
,可得∠COE=∠CPD,CP=CO,进而得到 ∠COP=∠COE,故可判断.
①正确,理由如下:
∵![]() ,
,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
又∵CA=CB,CD=CE,
∴![]() (SAS),
(SAS),
∴AD=BE,
故①正确;
②正确,理由如下:
由①知,![]() ,
,
∴∠CAD=∠CBE,
∵∠DOB为![]() 的外角,
的外角,
∴∠DOB=∠OBA+∠BAO=∠EBC+∠CBA+∠BAO=∠DAC+∠BAO+∠CBA=∠CBA+∠BAC,
∵∠CBA+∠BAC+∠ACB=180°,∠ACB=α,
∴∠CBA+∠BAC=180°-α,
即∠DOB=180°-α,
故②正确;
③错误,理由如下:
∵点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点,
的中点,
∴AM= ![]() AD,BN=
AD,BN= ![]() BE,
BE,
又∵由①知,AD=BE,
∴AM=BN,
又∵∠CAD=∠CBE,CA=CB,
∴![]() (SAS),
(SAS),
∴CM=CN,∠ACM=∠BCN,
∴∠MCN=∠MCB+∠CBN=∠MCB+∠ACM=∠ACB=α,
∴![]() 为等腰三角形且∠MCN=α,
为等腰三角形且∠MCN=α,
∴![]() 不是等边三角形,
不是等边三角形,
故③错误;
④正确,理由如下:

如图所示,在AD上取一点P使得DP=EO,连接CP,
由①知,![]() ,
,
∴∠CEO=∠CDP,
又∵CE=CD,EO=DP,
∴![]() (SAS),
(SAS),
∴∠COE=∠CPD,CP=CO,
∴∠CPO=∠COP,
∴∠COP=∠COE,
即OC平分∠AOE,
故④正确;
故答案为:B.