Question

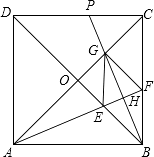
【题目】如图，正方形ABCD的对角线相交于点O，∠CAB的平分线分别交BD，BC于点E，F，作BH⊥AF于点H，分别交AC，CD于点G，P，连接GE，GF．

（1）求证：△OAE≌△OBG；
（2）试问：四边形BFGE是否为菱形？若是，请证明；若不是，请说明理由；
（3）试求： 的值（结果保留根号）．

Answer 1

【答案】
（1）

证明：∵四边形ABCD是正方形，

∴OA=OB，∠AOE=∠BOG=90°．

∵BH⊥AF，

∴∠AHG=90°，

∴∠GAH+∠AGH=90°=∠OBG+∠AGH，

∴∠GAH=∠OBG，即∠OAE=∠OBG．

∴在△OAE与△OBG中， ，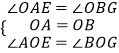

∴△OAE≌△OBG（ASA）

（2）

四边形BFGE是菱形，理由如下：

∵在△AHG与△AHB中，

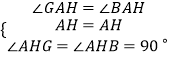
∴△AHG≌△AHB（ASA），

∴GH=BH，

∴AF是线段BG的垂直平分线，

∴EG=EB，FG=FB．

∵∠BEF=∠BAE+∠ABE=67.5°，∠BFE=90°﹣∠BAF=67.5°

∴∠BEF=∠BFE

∴EB=FB，

∴EG=EB=FB=FG，

∴四边形BFGE是菱形

（3）

设OA=OB=OC=a，菱形GEBF的边长为b．

∵四边形BFGE是菱形，

∴GF∥OB，

∴∠CGF=∠COB=90°，

∴∠GFC=∠GCF=45°，

∴CG=GF=b，

（也可由△OAE≌△OBG得OG=OE=a﹣b，OC﹣CG=a﹣b，得CG=b）

∴OG=OE=a﹣b，在Rt△GOE中，由勾股定理可得：2（a﹣b）2=b2，求得 a= b

∴AC=2a=（2+ ）b，AG=AC﹣CG=（1+ ）b

∵PC∥AB，

∴△CGP∽△AGB，

∴ = = = ﹣1，

由（1）△OAE≌△OBG得 AE=GB，

∴ = = ﹣1，即 = ﹣1．

【解析】（1）通过全等三角形的判定定理ASA证得：△OAE≌△OBG；（2）四边形BFGE是菱形．欲证明四边形BFGE是菱形，只需证得EG=EB=FB=FG，即四条边都相等的四边形是菱形；（3）设OA=OB=OC=a ， 菱形GEBF的边长为b．由该菱形的性质CG=GF=b，（也可由△OAE≌△OBG得OG=OE=a﹣b，OC﹣CG=a﹣b，得CG=b）；然后在Rt△GOE中，由勾股定理可得a= b，通过相似三角形△CGP∽△AGB的对应边成比例得到： = = ﹣1；最后由（1）△OAE≌△OBG得到：AE=GB，故 = = ﹣1．