题目内容
如右图所示,在梯形ABCD中,AD//BC,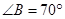 ,
,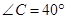 ,DE//AB交BC于点E。若AD=3,BC=10,则CD的长是( )
,DE//AB交BC于点E。若AD=3,BC=10,则CD的长是( )
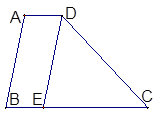
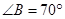 ,
,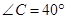 ,DE//AB交BC于点E。若AD=3,BC=10,则CD的长是( )
,DE//AB交BC于点E。若AD=3,BC=10,则CD的长是( )
| A.7 | B.10 | C.13 | D.14 |
A
根据平行线的性质,得∠DEC=∠B=70°,根据三角形的内角和定理,得∠CDE=70°,再根据等角对等边,得CD=CE.根据两组对边分别平行,知四边形ABED是平行四边形,则BE=AD=3,从而求解.
解:∵DE∥AB,∠B=70°,
∴∠DEC=∠B=70°.
又∵∠C=40°,
∴∠CDE=70°.
∴CD=CE.
∵AD∥BC,DE∥AB,
∴四边形ABED是平行四边形.
∴BE=AD=3.
∴CD=CE=BC-BE=BC-AD=10-3=7.
故选A.
此题综合运用了平行四边形的判定及性质、平行线的性质、等角对等边的性质.
解:∵DE∥AB,∠B=70°,
∴∠DEC=∠B=70°.
又∵∠C=40°,
∴∠CDE=70°.
∴CD=CE.
∵AD∥BC,DE∥AB,
∴四边形ABED是平行四边形.
∴BE=AD=3.
∴CD=CE=BC-BE=BC-AD=10-3=7.
故选A.
此题综合运用了平行四边形的判定及性质、平行线的性质、等角对等边的性质.

练习册系列答案
相关题目
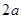 ,沿图中线段DE、CF将△ABC剪开,分成的三块图形恰能拼成正方形CFHG,如图1所示.请你解决如下问题:
,沿图中线段DE、CF将△ABC剪开,分成的三块图形恰能拼成正方形CFHG,如图1所示.请你解决如下问题: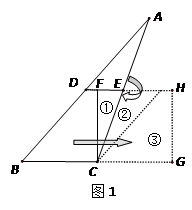
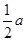 .请你设计两种不同的分割方法,将△A′B′C′沿分割线剪开后,所得的三块图形恰能拼成一个正方形,请在图2、图3中,画出分割线及拼接后的图形.
.请你设计两种不同的分割方法,将△A′B′C′沿分割线剪开后,所得的三块图形恰能拼成一个正方形,请在图2、图3中,画出分割线及拼接后的图形.
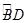 ,M是BC的中点,过点M作EM⊥BC交
,M是BC的中点,过点M作EM⊥BC交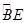 的长为 ★ .
的长为 ★ .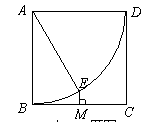
 度;
度;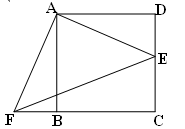
 ,如果点
,如果点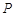 满足
满足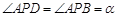 ,且
,且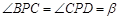 ,则称点
,则称点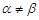 ;
;