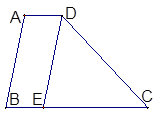
题目内容
已知：如图，梯形ABCD中，DC∥AB，AD=BC，对角线AC、BD交于点O，∠COD=60°，若CD=3，
AB=8，求梯形ABCD的高．
AB=8，求梯形ABCD的高．
解：过点C作CE∥DB，交AB的延长线于点E．
∴∠ACE=∠COD=60°．
又∵DC∥AB， ∴四边形DCEB为平行四边形．
∴BD=CE，BE =" DC" =3，AE=AB+BE=8+3=11．
又∵DC∥AB，AD=BC，
∴DB="AC" =CE．
∴△ACE为等边三角形．
∴AC=AE=11，∠CAB=60°．
过点C作CH⊥AE于点H．在Rt△ACH中，
CH=AC·sin∠CAB=11×
=
．
∴梯形ABCD的高为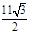
．
∴∠ACE=∠COD=60°．
又∵DC∥AB， ∴四边形DCEB为平行四边形．
∴BD=CE，BE =" DC" =3，AE=AB+BE=8+3=11．
又∵DC∥AB，AD=BC，
∴DB="AC" =CE．
∴△ACE为等边三角形．
∴AC=AE=11，∠CAB=60°．
过点C作CH⊥AE于点H．在Rt△ACH中，
CH=AC·sin∠CAB=11×
=．∴梯形ABCD的高为
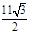． 略
练习册系列答案
津桥教育计算小状元系列答案
相关题目
为正方形
对角线AC上一点，以
长为半径的⊙
相切于点
.
与⊙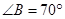
,
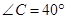,DE//AB交BC于点E。若AD=3，BC=10，则CD的长是（ ）
