Question

【题目】如图，在△ABC中，BD平分∠ABC交AC于D，EF垂直平分BD，分别交AB，BC，BD于E，F，G，连接DE，DF．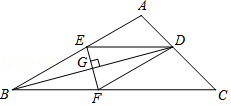
（1）求证：DE=DF；
（2）若∠ABC=30°，∠C=45°，DE=4，求CF的长．

Answer 1

【答案】
（1）证明：∵EF垂直平分BD，

∴EB=ED，FB=FD．

∵BD平分∠ABC交AC于D，

∴∠ABD=∠CBD．

∵∠ABD+∠BEG=90°，∠CBD+∠BFG=90°，

∴∠BEG=∠BFG．

∴BE=BF．

∴四边形BFDE是菱形．

∴DE=DF

（2）解：过D作DH⊥CF于H．

∵四边形BFDE是菱形，

∴DF∥AB，DE=DF=4．

在Rt△DFH中，∠DFC=∠ABC=30°，

∴DH=2，FH= DH=2 ，

在Rt△CDH中，∠C=45°，

∴DH=HC=2，

∴CF=CH+FH=2+2 ．

【解析】（1）只要证明四边形BFDE是菱形即可；（2）在Rt△DFH中，求出DH、FH，在Rt△DHC中，求出CH即可解决问题；