题目内容
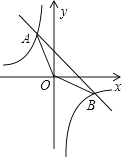
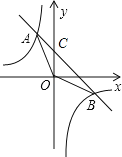
【题目】如图,一次函数y=kx+b的图象与反比例函数y=﹣![]() 的图象交于A、B两点,A的横坐标和点B的纵坐标都是﹣2.求:
的图象交于A、B两点,A的横坐标和点B的纵坐标都是﹣2.求:
(1)一次函数的表达式;
(2)△AOB的面积;
(3)根据图象,当x在什么范围内时,一次函数的值大于反比例函数的值?
【答案】(1)y=﹣x+2;(2)6;(3)x<﹣2和0<x<4.
【解析】
试题分析:(1)由反比例函数解析式可分别求得A、B两点的坐标,再利用待定系数法可求得一次函数表达式;
(2)设直线一次函数与y轴交于C点,可求得C点坐标,再利用三角形的面积公式计算即可;
(2)一次函数的值大于反比例函数的值时即一次函数的图象在反比例函数图象的上方,结合图象可求得x的范围.
解:
(1)反比例函数y=﹣![]() 的图象交于A、B两点,且A的横坐标和点B的纵坐标都是﹣2,
的图象交于A、B两点,且A的横坐标和点B的纵坐标都是﹣2,
∴A点的纵坐标为和B点的横坐标都为4,
∴A(﹣2,4),B(4,﹣2),
∵一次函数y=kx+b的图象过A、B两点,
∴把A、B两点坐标代入可得![]() ,解得
,解得![]() ,
,
∴一次函数表达式为y=﹣x+2;
(2)如图,设一次函数与y轴交于点C,则C点坐标为(0,2),
∴OC=2,
∴S△AOB=S△AOC+S△BOC=![]() OC2+
OC2+![]() OC4=6;
OC4=6;
(3)结合图象可知一次函数的图象在反比例函数图象的上方时,对应的x的取值范围为x<﹣2和0<x<4,
∴一次函数的值大于反比例函数的值时对应的x的取值范围为x<﹣2和0<x<4.

【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?