题目内容
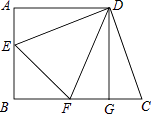
【题目】如图,正方形ABCD中,边长为12,DE⊥DC交AB于点E,DF平分∠EDC交BC于点F,连接EF. 
(1)求证:EF=CF;
(2)当 ![]() =
= ![]() 时,求EF的长.
时,求EF的长.
【答案】
(1)证明:∵正方形ABGD,
又∵DE⊥DC,
∴∠ADE+∠EDG=90°=∠GDC+∠EDG,
∴∠ADE=∠GDC.
又∵∠A=∠DGC,
且AD=GD,
在△ADE与△GDC中,
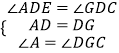 ,
,
∴△ADE≌△GDC(ASA).
∴DE=DC,且AE=GC.
在△EDF和△CDF中,
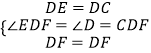 ,
,
∴△EDF≌△CDF(SAS).
∴EF=CF
(2)解:∵ ![]() =
= ![]() ,
,
∴AE=GC=4.
设EF=x,则BF=16﹣CF=16﹣x,BE=12﹣4=8.
由勾股定理,得x2=(16﹣x)2+82.
解之,得x=10,
即EF=10
【解析】(1)根据正方形的性质和全等三角形的判定和性质证明即可;(2)设EF=x,根据勾股定理解答即可.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目