题目内容
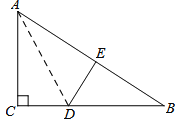
【题目】如图,在△ABC中,AB=4 cm,AC=2 cm.
(1)在AB上取一点D(D不与A、B重合),当AD=_________cm时,△ACD∽△ABC.
(2)在AC的延长线上取一点E,当CE=________cm时,△AEB∽△ABC.此时BE与DC有怎样的位置关系?为什么?
【答案】(1)1; (2)6.
【解析】(1)如图,∵∠A=∠A,∴当AD:AC=AC:AB时,△ACD∽△ABC.
由AD:AC=AC:AB可得:AD·AB=AC2,∵AC=2,AB=4,∴解得AD=1,即当AD=1时,AD:AC=AC:AB;
(2)如图,∵∠A=∠A,∴当AE:AB=AB:AC时,△AEB∽△ABC.
由AE:AB=AB:AC可得AE·AC=AB2,∵AC=2,AB=4,∴AE=8,∴CE=AE-AC=6.
此时,BE∥CD,理由如下:
∵△ACD∽△ABC,△AEB∽△ABC,
∴∠ACD=∠ABC,∠AEB=∠ABC,
∴∠ACD=∠AEB,
∴BE∥CD.


练习册系列答案
相关题目
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
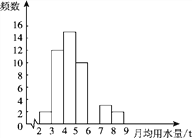
(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.