题目内容
【题目】探究与发现:
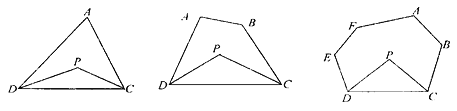
图1 图2 图3
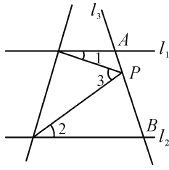
(1)探究一:三角形的一个内角与另两个内角的平分线所夹的角之间的关系
已知:如图1,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系,并说明理由.
(2)探究二:四边形的两个个内角与另两个内角的平分线所夹的角之间的关系
已知:如图2,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,
试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)探究三:六边形的四个内角与另两个内角的平分线所夹的角之间的关系
已知:如图3,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:__ __ __.
【答案】(1)∠P=90°+![]() ∠A (2) ∠P=
∠A (2) ∠P=![]() (∠A+∠B)(3)∠P=
(∠A+∠B)(3)∠P=![]() (∠A+∠B+∠E+∠F)-180°
(∠A+∠B+∠E+∠F)-180°
【解析】试题分析:探究一:根据角平分线的定义可得∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,然后根据三角形内角和定理列式整理即可得解;
∠ACD,然后根据三角形内角和定理列式整理即可得解;
探究二:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;
探究三:根据六边形的内角和公式表示出∠ADC+∠BCD,然后同理探究二解答即可.
试题解析:探究一:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠DPC=180°-∠PDC-∠PCD,
=180°-![]() ∠ADC-
∠ADC-![]() ∠ACD,
∠ACD,
=180°-![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°-![]() (180°-∠A),
(180°-∠A),
=90°+![]() ∠A;
∠A;
探究二:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠DPC=180°-∠PDC-∠PCD,
=180°-![]() ∠ADC-
∠ADC-![]() ∠BCD,
∠BCD,
=180°-![]() (∠ADC+∠BCD),
(∠ADC+∠BCD),
=180°-![]() (360°-∠A-∠B),
(360°-∠A-∠B),
=![]() (∠A+∠B);
(∠A+∠B);
探究三:六边形ABCDEF的内角和为:(6-2)180°=720°,
∵DP、CP分别平分∠ADC和∠ACD,
∴∠P=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠P=180°-∠PDC-∠PCD,
=180°-![]() ∠ADC-
∠ADC-![]() ∠ACD,
∠ACD,
=180°-![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°-![]() (720°-∠A-∠B-∠E-∠F),
(720°-∠A-∠B-∠E-∠F),
=![]() (∠A+∠B+∠E+∠F)-180°,
(∠A+∠B+∠E+∠F)-180°,
即∠P=![]() (∠A+∠B+∠E+∠F)-180°.
(∠A+∠B+∠E+∠F)-180°.
考点: 1.多边形内角与外角;2.三角形内角和定理.

 备战中考寒假系列答案
备战中考寒假系列答案