Question

【题目】如图，在Rt△ABC中，∠C=，△ACD沿AD折叠，使得点C落在斜边AB上的点E处．

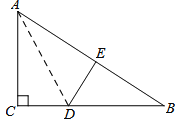
（1）问：△BDE与△BAC相似吗？

（2）已知AC=6，BC=8，求线段AD的长度．

Answer 1

【答案】（1）相似；（2）3.

【解析】试题分析： （1）根据折叠的性质得出∠C=∠AED=，利用∠DEB=∠C，∠B=∠B证明三角形相似；（2）先由勾股定理求出AB的长，再由折叠的性质知DE=CD，AE=AC，BE=AB-AE，在Rt△BDE中运用勾股定理求出DE，即CD，最后在Rt△ACD中运用勾股定理得出AD．

试题解析：（1）相似．理由如下：

∵∠C=，△ACD沿AD折叠，使得点C落在斜边AB上的点E处，

∴∠C=∠AED=，

∴∠DEB=∠C=，

∵∠B=∠B，

∴△BDE∽△BAC；

（2）由勾股定理，得

AB==10．

由折叠的性质知，AE=AC=6，DE=CD，∠AED=∠C=．

∴BE=AB-AE=10-6=4，

在Rt△BDE中，由勾股定理得，

，

即，

解得：CD=3，

在Rt△ACD中，由勾股定理得

即，

解得：AD=3.