题目内容
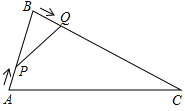
【题目】已知:如图,AE2=AD·AB,且∠ABE=∠ACB.
证明:(1)△ADE∽△AEB; (2)DE∥BC; (3)△BCE∽△EBD.

【答案】详见解析.
【解析】试题分析:
(1)由AE2=AD·AB可得:AE:AB=AD:AE,结合∠A=∠A,可得△ADE∽△AEB;
(2)由△ADE∽△AEB可得:∠AED=∠ABE,结合∠ABE=∠ACB,可得∠AED=∠ACB,从而由平行线的判定可得DE∥BC;
(3)由DE∥BC可得∠EBC=∠DEB,结合∠ABE=∠ACB,可得△BCE∽△EBD.
试题解析:
(1)∵AE2=AD·AB,
∴AE:AB=AD:AE,
又∵∠A=∠A,
∴△ADE∽△AEB.
(2)∵△ADE∽△AEB,
∴∠AED=∠ABE,
又∵∠ABE=∠ACB,
∴∠AED=∠ACB,
∴DE∥BC.
(3)∵DE∥BC,
∴∠EBC=∠DEB,
又∵∠ABE=∠ACB,
∴△BCE∽△EBD.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目