��Ŀ����
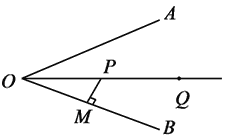
����Ŀ����֪��BOA��һ����·������OPǡ�þ�����Oƽ�֡�AOB��
��1�����Ҫ��P���ƶ�����·��·����̣���ͼ����ʾPM�⣬������ѡ��PN����������·��������·���Ĺ�ϵ��______��������___________��
��2���������δ���һ��Q�����Ҫ��P����������﹫·OA�ϵĵ�C����ǰ����Q�����㻭��һ�����·����������C��λ�ã�
��3��D���ڹ�·OB�ϣ�O�㵽D��ľ�����C����ȣ�������CDP����֤����CDPΪ���������Σ�
���𰸡���1���Գƣ��㵽ֱ�ߵľ��룬���߶���̣���2����ͼ����������3��֤����������
��������
��1������P��OA�Ĵ����ɵã�
��2������P����OA�ĶԳƵ�P��������P��Q����OA�Ľ��㼴Ϊ�����C��
��3������C��OQ�Ĵ��ߣ���OB�ڵ�D�������д��ߺͽ�ƽ���ߵ�����֤�����ɵã�
��1���߶�PNΪ����

��2��P��C��Q·����̣���C��Ϊ����

��3����ͼ����CDP��Ϊ����

������ã�
OC=OD����AOQ=��BOQ��OP=OP��
���COP�ա�DOP��SAS����
��CP=DP��
���CDP����������

��ϰ��ϵ�д�
�����Ŀ