题目内容
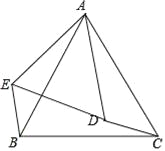
【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

【答案】(1)证明见解析;(2)∠BED=45°.
【解析】试题分析:(1)由等边三角形的性质知∠BAC=60°,AB=AC,由旋转的性质知∠DAE=60°,AE=AD,从而得∠EAB=∠DAC,再证△EAB≌△DAC可得答案;
(2)由∠DAE=60°,AE=AD知△EAD为等边三角形,即∠AED=60°,继而由∠AEB=∠ADC=105°可得.
试题解析:(1)∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC.
∵线段AD绕点A顺时针旋转60°,得到线段AE,
∴∠DAE=60°,AE=AD.
∴∠BAD+∠EAB=∠BAD+∠DAC.
∴∠EAB=∠DAC.
在△EAB和△DAC中,
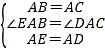 ,
,
∴△EAB≌△DAC.
∴∠AEB=∠ADC.
(2)如图,

∵∠DAE=60°,AE=AD,
∴△EAD为等边三角形.
∴∠AED=60°,
又∵∠AEB=∠ADC=105°.
∴∠BED=45°.

 阅读快车系列答案
阅读快车系列答案【题目】【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长
最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数表达式为y=2(x+ ![]() )(x>0).
)(x>0).
【探索研究】
小彬借鉴以前研究函数的经验,先探索函数y=x+ ![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数y=x+ ![]() 的自变量x的取值范围是x>0,如表是y与x的几组对应值.
的自变量x的取值范围是x>0,如表是y与x的几组对应值.
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①写出m的值;
②画出该函数图象,结合图象,得出当x=时,y有最小值,y最小=;
(2)【解决问题】
直接写出“问题情境”中问题的结论.