题目内容
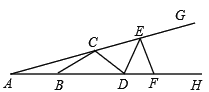
【题目】如图，在ABCD中，AE⊥BC于点E点，延长BC至F点使CF=BE，连接AF，DE，DF． 
（1）求证：四边形AEFD是矩形；
（2）若AB=6，DE=8，BF=10，求AE的长．
【答案】
（1）解：证明：∵CF=BE，
∴CF+EC=BE+EC．
即 EF=BC．
∵在ABCD中，AD∥BC且AD=BC，
∴AD∥EF且AD=EF．
∴四边形AEFD是平行四边形．
∵AE⊥BC，
∴∠AEF=90°．
∴四边形AEFD是矩形
（2）解：∵四边形AEFD是矩形，DE=8，
∴AF=DE=8．
∵AB=6，BF=10，
∴AB2+AF2=62+82=100=BF2．
∴∠BAF=90°．
∵AE⊥BF，
∴△ABF的面积= 
ABAF= BFAE．
∴AE= 
= 
= 
．
【解析】（1）先证明四边形AEFD是平行四边形，再证明∠AEF=90°即可．（2）证明△ABF是直角三角形，由三角形的面积即可得出AE的长．
【考点精析】根据题目的已知条件，利用平行四边形的性质的相关知识可以得到问题的答案，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
【题目】某销售公司为了提高员工的工作积极性，对员工的工资结构进行改革，改革后月工资由基本保障工资与计件奖励工资组成．（计件奖励工资＝销售每件的奖励金额×销售的件数）下表是甲、乙两位职工今年三月份的工资情况信息：
职工 | 甲 | 乙 |
月销售件数（件） | 100 | 80 |
月工资（元） | 4500 | 4100 |
求员工的月基本保障工资和销售每件产品的奖励金额各多少元？
