Question

【题目】如图，在梯形ABCD中，已知AD∥BC，∠B=90°，AB=7，AD=9，BC=12，在线段BC上任取一点E，连接DE，作EF⊥DE，交直线AB于点F．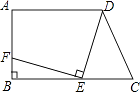
（1）若点F与B重合，求CE的长；
（2）若点F在线段AB上，且AF=CE，求CE的长；
（3）设CE=x，BF=y，写出y关于x的函数关系式（直接写出结果可）．

Answer 1

【答案】
（1）解：∵F与B重合，且EF⊥DE，

∴DE⊥BC，

∵AD∥BC，∠B=90°，

∴∠A=∠B=90°，

∴四边形ABED为矩形，

∴BE=AD=9，

∴CE=12﹣9=3

（2）解：作DH⊥BC于H，

则DH=AB=7，CH=3．

设AF=CE=x，

∵F在线段AB上，

∴点E在线段BH上，CH=3，CE=x，

∴HE=x﹣3，BF=7﹣x，

∵∠BEF+90°+∠HED=180°，∠HDE+90°+∠HED=180°，

∴∠BEF=∠HDE，

又∵∠B=∠DHE=90°，

∴△BEF∽△HDE，

∴ ，

∴ ，

整理得x2﹣22x+85=0，

（x﹣5）（x﹣17）=0，

∴x=5或17，

经检验，它们都是原方程的解，但x=17不合题意，舍去．

∴x=CE=5．

（3）解：作DH⊥BC于H，

∵AD∥BC，∠B=90°，AB=7，AD=9，BC=12，CE=x，BF=y，

∴则HE=x﹣3，BF=y，

当3≤x≤12时，

易证△BEF∽△HDE，

∴ = ，

∴y=﹣ x2+ x﹣ ，

当0≤x＜3，

易证△BEF∽△HDE，

则HE=3﹣x，BF=y，

∴ = ，

∴y= x2﹣ x+ ，

∴y= ．

【解析】（1）先证明四边形ABED为矩形，CE=BC﹣AD，继而即可求出答案；（2）设AF=CE=x，则HE=x﹣3，BF=7﹣x，再通过证明△BEF∽△HDE，根据对应边成比例，然后代入求解即可；（3）综合（1）（2）两种情况，然后代入求出解析式即可．
【考点精析】利用直角梯形和相似三角形的判定与性质对题目进行判断即可得到答案，需要熟知一腰垂直于底的梯形是直角梯形；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．