题目内容
【题目】在△ABC中,点D、E分别在边AC、BC上(不与点A、B、C重合),点P是直线AB上的任意一点(不与点A、B重合).设∠PDA=x,∠PEB=y,∠DPE=m,∠C=n.
(1)如图,当点P在线段AB上运动,且n=90°时
①若PD∥BC,PE∥AC,则m=_____;
②若m=50°,求x+y的值.
(2)当点P在直线AB上运动时,直接写出x、y、m、n之间的数量关系.


【答案】(1)①90°,②140°;(2)详见解析.
【解析】分析:(1)①证明四边形DPEC为平行四边形可得结论;
②根据四边形内角和为360°,列等式求出x+y的值;
(2)根据P、D、E位置的不同,分五种情况:①y-x=m+n,如图2,点P在BA的延长线上时,根据三角形的内角和与外角定理列等式,化简后得出结论;
②x-y=m-n,如图3,点P在BA的延长线上时,根据三角形的内角和与外角定理列等式,化简后得出结论;
③x+y=m+n,如图4,点P在线段BA上时,根据四边形的内角和为360°列等式,化简后得出结论;
④x-y=m+n,如图5,同理得出结论;
⑤y-x=m-n,如图6,同理得出结论.
详解:(1)①如图1,
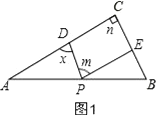
∵PD∥BC,PE∥AC,
∴四边形DPEC为平行四边形,
∴∠DPE=∠C,
∵∠DPE=m,∠C=n=90°,
∴m=90°;
②∵∠ADP=x,∠PEB=y,
∴∠CDP=180°-x,∠CEP=180°-y,
∵∠C+∠CDP+∠DPE+∠CEP=360°,
∠C=90°,∠DPE=50°,
∴90°+180°-x+50°+180°-y=360°,
∴x+y=140°;
(2)分五种情况:
①y﹣x=m+n,如图2,
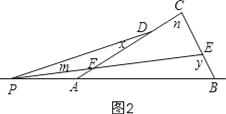
理由是:
∵∠DFP=n+∠FEC,∠FEC=180°﹣y,
∴∠DFP=n+180°﹣y,
∵x+m+∠DFP=180°,
∴x+m+n+180°﹣y=180°,
∴y﹣x=m+n;
②x﹣y=m﹣n,如图3,
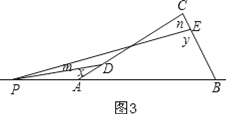
理由是:
同理得:m+180°﹣x=n+180°﹣y,
∴x﹣y=m﹣n;
③x+y=m+n,如图4,
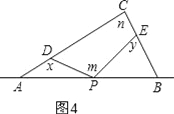
理由是:
由四边形内角和为360°得:180°﹣x+m+180°﹣y+n=360°,
∴x+y=m+n;
④x﹣y=m+n,如图5,
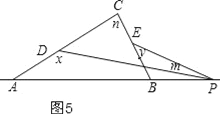
理由是:
同理得:180°=m+n+y+180°﹣x,
∴x﹣y=m+n;
⑤y﹣x=m﹣n,如图6,
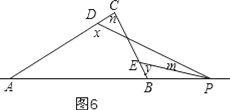
理由是:
同理得:n+180°﹣x=m+180°﹣y,
∴y﹣x=m﹣n.

 阅读快车系列答案
阅读快车系列答案