题目内容
【题目】问题情景：
如图1，AB//CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．
小明的思路是：
过点P作PE//AB，
∴∠PAB+∠APE=180°．
∵∠PAB=130°，∴∠APE=50°
∵AB//CD，PE//AB，∴PE//CD，
∴∠PCD+∠CPE=180°．
∵∠PCD=120°，∴∠CPE=60°
∴∠APC=∠APE+∠CPE=110°．
问题迁移：
如果AB与CD平行关系不变，动点P在直线AB、CD所夹区域内部运动时，∠PAB，∠PCD的度数会跟着发生变化．
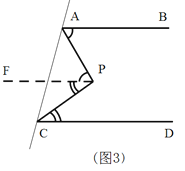
（1）如图3，当动点P运动到直线AC右侧时，请写出∠PAB，∠PCD和∠APC之间的数量关系？并说明理由．
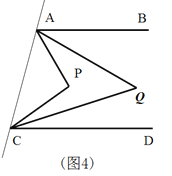
（2）如图4，AQ，CQ分别平分∠PAB，∠PCD，那么∠AQC和角∠APC有怎择的数量关系？
（3）如图5，点P在直线AC的左侧时，AQ，CQ仍然平分∠PAB，∠PCD，请直接写出∠AQC和角∠APC的数量关系 ．
【答案】(1) ∠PAB+∠PCD=∠APC．(2)∠AQC=
∠APC;(3) 2∠AQC+∠APC=360°．
【解析】分析：（1）过点P作PF∥AB，由平行线的传递性得到PF∥CD，再由两直线平行，内错角相等即可得出结论；
（2）由（1）的结论得到∠PAB+∠PCD=∠APC， ∠QAB+∠QCD=∠AQC，再由角平分线的性质即可得到结论；
（3）由（1）得：∠BAQ+∠CDQ=∠AQC．再由角平分线的性质得到∠PAQ+∠PCQ=∠AQC，根据四边形内角和为360°即可得到结论．
详解：（1）∠PAB+∠PCD=∠APC．
理由：如图3，过点P作PF∥AB，∴∠PAB=∠APF．
∵AB∥CD，PF∥AB，∴PF∥CD，
∴∠PCD=∠CPF，∴∠PAB+∠PCD=∠APF+∠CPF=∠APC，
即∠PAB+∠PCD=∠APC．
（2）
．
理由：如图4．
∵AQ，CQ分别平分∠PAB，∠PCD，
∴∠QAB=∠PAB，∠QCD=∠PCD，
∴∠QAB+∠QCD=∠PAB+∠PCD=（∠PAB+∠PCD），
由（1），可得∠PAB+∠PCD=∠APC，
∠QAB+∠QCD=∠AQC
∴∠AQC=∠APC．
（3）2∠AQC+∠APC=360°．理由如下：
由（1）得：∠BA Q+∠CDQ=∠AQC．
∵AQ平分∠PAB，CQ平分∠PCD，∴∠PAQ=∠BAQ，∠PCQ=∠DCQ，∴∠PAQ+∠PCQ=∠AQC．
∵∠PAQ+∠PCQ+∠AQC+∠APC=360°，∴∠APC+2∠AQC=360°．
