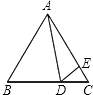题目内容
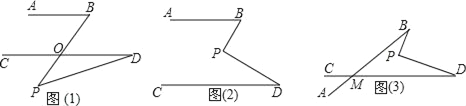
【题目】(1)如图(1),AB∥CD,点P在AB,CD外部,若∠B=50°,∠D=25°,则∠BPD= °
(2)如图(2),AB∥CD,点P在AB,CD内部,则∠B,∠D,∠BPD之间有何数量关系?证明你的结论.
(3)在图(2)中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M,如图(3),若∠BPD=90°,∠BMD=40°,求∠B+∠D的度数.
【答案】(1)25(2)∠B+∠D=∠BPD(3)50°
【解析】分析:(1)由,,根据两直线平行,内错角相等,即可求得的度数,又由三角形外角的性质,可求得的度数;(2)首先过点P作,由,可得,然后由两直线平行,内错角相等,即可证得;
(3)首先延长BP交CD于点E,利用三角形外角的性质,即可求得的度数.
详解:(1)解:∵AB∥CD,
∴∠BOD=∠B=50°,
由三角形的外角性质得,∠BPD=∠BOD﹣∠D=50°﹣25°=25°;
故答案为:25.
(2)解:∠B+∠D=∠BPD.
理由如下:如图,延长BP交CD于E,
∵AB∥CD,
∴∠BED=∠B,
由三角形的外角性质得,∠BED+∠D=∠BPD,
所以,∠B+∠D=∠BPD;
(3)解:如图,延长BP交CD于E,
由三角形的外角性质得,∠BED=∠B+∠BMD,
∠BPD=∠BED+∠D,
所以,∠BPD=∠B+∠BMD+∠D,
∵∠BPD=90°,∠BMD=40°,
∴90°=∠B+40°+∠D,
解得∠B+∠D=50°.


练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目