��Ŀ����
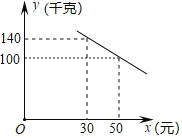
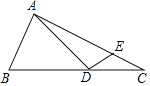
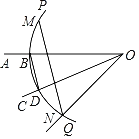
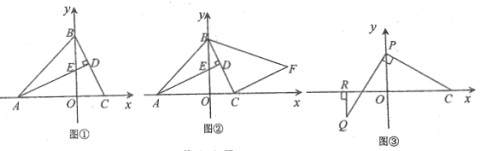
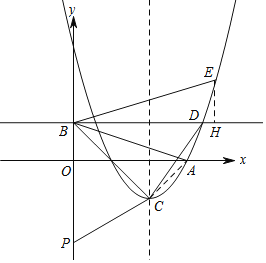
����Ŀ����ƽ��ֱ������ϵxOy�У���ͼ������֪��A��x����������ϣ�����ԭ��ľ���Ϊ3��������y��ax2��4ax+3��a��0��������A���䶥��ΪC��ֱ��y��1��y�ύ�ڵ�B���������߽��ڵ�D������Գ����Ҳࣩ������BC��CD��
��1���������ߵı���ʽ����C�����ꣻ
��2����P��y��ĸ������ϵ�һ�㣬�����PBC���BCD���ƣ������ƱȲ�Ϊ1�����P�����ꣻ
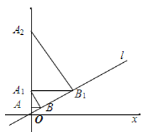
��3������CBD���ŵ�B��ʱ�뷽����ת��ʹ����BC������A����һ���������߽��ڵ�E����E�ڶԳ�����Ҳࣩ�����E�����꣮
���𰸡���1��y��x2��4x+3��C��2����1������2��P��0��4![]() ��7������3��E��4��3��
��7������3��E��4��3��
��������
��1���ѵ�A��������������ߵĽ���ʽ�пɵã�a��ֵ���Ӷ��������ߵĽ���ʽ���䷽�ö���C�����ꣻ
��2�����ݡ�DBC����PBC��45�㣬�����ƱȲ�Ϊ1������ֻ�ܡ�CBP�ס�DBC���б���ʽ�ɵ�BP�ij����Ӷ��õ�P�����ꣻ
��3������AC����E��EH��BD��H���ȸ��ݹ��ɶ������涨��֤����ABC�ǵ���ֱ�������Σ��ҡ�ACB��90�㣬�ɵȽ����Ǻ�����tan��ABC��tan��EBD��![]() ��
��![]() ����EH��m����BH��2m����ʾE��2m��m+1�������������ߵĽ���ʽ���ɵý��ۣ�
����EH��m����BH��2m����ʾE��2m��m+1�������������ߵĽ���ʽ���ɵý��ۣ�
�⣺��1���ߵ�A��x����������ϣ�����ԭ��ľ���Ϊ3��
��A��3��0����
��A��3��0������������y��ax2��4ax+3�еã�0��9a��12a+3��
��a��1��
�������ߵı���ʽΪ��y��x2��4x+3��
y��x2��4x+3����x��2��2��1��
��C��2����1����
��2����y��1ʱ��x2��4x+3��1��
��ã�x1��2��![]() ��x2��2+
��x2��2+![]() ��
��
������ã�D��2+![]() ��1����
��1����
��B��0��1����C��2����1����
��BC��![]() ��2
��2![]() ��BD��2+
��BD��2+![]() ��
��
�ߡ�DBC����PBC��45�㣬�����ƱȲ�Ϊ1��
ֻ�ܡ�CBP�ס�DBC��
��![]() ����
����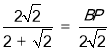 ��
��
��BP��8��4![]() ��
��
��P��0��4![]() ��7����
��7����
��3������AC����E��EH��BD��H��
����ת�ã���CBD����ABE��
���EBD����ABC��
��AB2��32+12��10��BC2��22+22��4��AC2��12+12��2��
��AB2��BC2+AC2��
���ABC�ǵ���ֱ�������Σ��ҡ�ACB��90�㣬
��tan��ABC��![]() ��
��![]() ��
��
��tan��EBD��![]() ��
��![]() ��
��
��EH��m����BH��2m��
��E��2m��m+1����
�ߵ�E���������ϣ�
�ࣨ2m��2��4��2m+3��m+1��
4m2��9m+2��0��
��ã�m1��2��m2��![]() ���ᣩ��
���ᣩ��
��E��4��3����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��Сӱ���ۺ���ʵ����С��ѧϰ�����Ǻ�����չ�˲�����У��˸߶ȵ�ʵ����������ƶ��˲��������������ÿ���ʱ�������ʵ�ز����������ڸ���˵ײ����ڵ�ƽ���ϣ�ѡȡ������ͬ��㣬�ֱ�����˸���˶��˵������Լ����������֮��ľ��룮Ϊ�˼�С������С���ڲ������ǵĶ����Լ��������֮��ľ���ʱ�����ֱ���������β�ȡ���ǵ�ƽ��ֵ��Ϊ�������������Dz������������ݣ�
���� | ������˵ĸ߶� | |||
��Ա | �鳤��Сӱ����Ա��С����С�գ�СӢ | |||
�������� | �����Ƕȵ�������Ƥ�ߵ� | |||
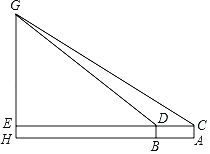
����ʾ��ͼ |
| ˵���� �߶�GH��ʾѧУ��ˣ������Ƕȵ������ĸ߶�AC��BD��1.62m�����A��B��H��ͬһˮƽֱ���ϣ�A��B֮��ľ������ֱ�Ӳ�ã��ҵ�G��H��A��B��C��D����ͬһ��ֱƽ���ڣ���C��D��E��ͬһ��ֱ���ϣ���E��GH�ϣ� | ||
�������� | ������Ŀ | ��һ�� | �ڶ��� | ƽ��ֵ |
��GCE�Ķ��� | 30.6�� | 31.4�� | 31�� | |
��GDE�Ķ��� | 36.8�� | 37.2�� | 37�� | |
A��B֮��ľ��� | 10.1m | 10.5m | �� ��m | |
�� | �� | |||
��1������һ����ɱ��������β��A��B֮��ľ����ƽ��ֵ��
��2����������������ϲ����������������á��ۺ���ʵ����С�����ѧУ���GH�ĸ߶ȣ�����ȷ��0.1m�����ο����ݣ�sin31����0.51��cos31����0.86��tan31����0.60��sin37����0.60��cos37����0.80��tan37����0.75��