Question

【题目】已知，是⊙O的直径，弦垂直平分，垂足为，连接．

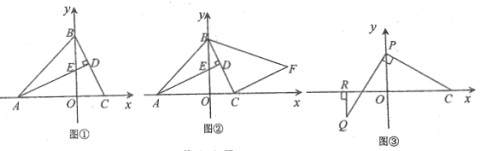
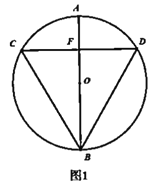
（1）如图1，求的度数；

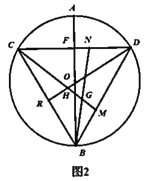
（2）如图2，点分别为上一点，并且，连接，交点为G，R为上一点，连接与交于点H，，求证：；

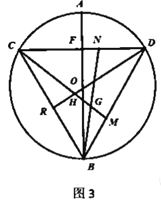
（3）如图3，在（2）的条件下，，求⊙O半径．

Answer 1

【答案】（1）60°；

（2）证明见解析；

（3）半径为．

【解析】

（1）根据垂直平分线的性质和圆的半径相等可得出是等边三角形，再根据同弧所对的圆周角相等即可求出答案；

（2）垂直平分，是等边三角形，得出△BCD是等边三角形，得到BD=BC，∠CBM=∠BDN，再证明，根据外角设，找到即可求出结论．

（3）在（2）的条件下，做辅助线：作CP⊥BN，DQ⊥CM，翻折DH到DT；求出，再根据角的关系得到∠DHT=∠CDT=∠T即，由勾股定理求出DC即可求解半径．

（1）证明：

连接

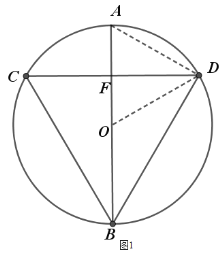
∵垂直平分，

又

是等边三角形

∵ ,

（2）证明：

∵垂直平分，

∴,AB⊥CD，

∴∠ABC=∠ABD，BC=BD，

∵是等边三角形，

∴∠AOD=60°，

∴∠DBC=60°，

∴△BCD是等边三角形，

∴BD=BC，∠CBM=∠BDN，

∵

∴，

∴∠BCM=∠DBN，

∵∠DBN+∠CBN=60°，

∴∠BCM+∠CBN=60°，

∵∠BGM是△BGC的一个外角，

∴，

设，

∵，

∴，

，

∵∠DHM是△DHC的一个外角，

∴，

∴．

（3）如图：连接AC，作CP⊥BN，DQ⊥CM，翻折DH到DT；

①在中：

，，

勾股定理得，

②∵BC=CD，∠DCM=∠CBP，∠CPB=∠CQD=90°，

，

得，

翻折得，

∵，

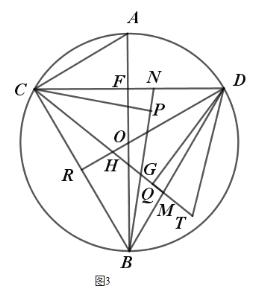
∴∠DHT=∠DCM+∠CDR=60°-∠BCM+ =60°+，

∴，

∵∠CDT=∠CDR+∠HDT

∴∠CDR+2（90°-∠DHT）=∠CDR+2（30°-∠BCM）=60°+，

∴∠DHT=∠CDT=∠T，

得

③设，

在中，

，

，

得，

由（1）得∠ACF=30°，∠A=60°，

∴AC= ，

∵ ,

∴AC=，

即半径为；