题目内容
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,连接
运动,连接![]() 交
交![]() 于点
于点![]() .
.
(![]() )试证明:无论点
)试证明:无论点![]() 运动到
运动到![]() 上何处时,都有
上何处时,都有![]() ≌
≌![]() .
.
(![]() )若点
)若点![]() 从点
从点![]() 运动到点
运动到点![]() ,再继续在
,再继续在![]() 上运动到点
上运动到点![]() ,在整个运动过程中,点
,在整个运动过程中,点![]() 以每秒
以每秒![]() 单位长度的速度匀速运动,当
单位长度的速度匀速运动,当![]() 恰为等腰三角形,求点
恰为等腰三角形,求点![]() 运动的时间.
运动的时间.
【答案】(1)证明见解析;(2)点![]() 运动时间分别为
运动时间分别为![]() ,
, ![]() ,
, ![]() .
.
【解析】试题分析:(1)根据SAS证明即可;(2)分别讨论当AD=DQ,AD=AQ,AQ=DQ三种情况.
解:(1)在正方形ABCD中,AB=AD,∠DAC=∠BAC,
在△ADQ和△ABQ中,AD=AB,∠DAC=∠BAC,AQ=AQ,∴△ADQ≌△ABQ.
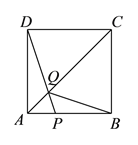
(2)①如图①中,当AQ=DQ时,∠QDA=∠QAD=45°,则点Q为正方形ABCD的中心,点B与点P重合,此时点P运动的时间为t1=4÷1=4(s);

②图②中,当AQ=AD时,则∠ADQ=∠AQD,
∵正方形ABCD边长为4,∴AC![]() ,
,
∴CQ=AC-AQ=![]() ,
,
∵AD∥BC,∴∠CPQ=∠ADQ,
∴∠CPQ=∠AQD=∠CQP,∴CP=CQ=![]() ,
,
∴BP=![]() ,
,
∴P点运动的时间为t2=(4+8-![]() )÷1
)÷1![]() .
.
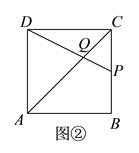
(3)如图③,当AD=DQ时,点C,P,Q三点重合,
此时P点运动时间为t3=(4+4)÷1=8(s).
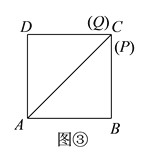
综上,当△ADQ恰为等腰三角形时,点P运动时间可以为4s, ![]() ,8s.
,8s.

练习册系列答案
相关题目