题目内容
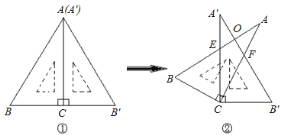
【题目】将两块大小相同的含30°角的直角三角板(![]() =30°)按图1的方式放置,固定三角板ABC然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图2所示的位置,AB与AC交于点E,AC与AB交于点F,AB与AB交于点O.
=30°)按图1的方式放置,固定三角板ABC然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图2所示的位置,AB与AC交于点E,AC与AB交于点F,AB与AB交于点O.
(1)求证:![]() ;
;
(2)当旋转角等于30°时,AB与AB垂直吗?请说明理由。
【答案】(1)见解析;(2)AB与A1B1垂直,理由见解析
【解析】
(1)根据题意可知∠B=∠B1,BC=B1C,∠BCE=∠B1CF,利用ASA即可证出△BCE≌△B1CF;
(2)由旋转角等于30°得出∠ECF=30°,所以∠FCB1=60°,根据四边形的内角和可知∠BOB1的度数为360°-60°-60°-150°,最后计算出∠BOB1的度数即可.
(1)证明:由题意得,BC=B1C,∠B=∠B1=60°,
又∵∠BCE+∠ECF=90°,
∠B1CF+∠ECF=90°,
∴∠BCE=∠B1CF,
在△BCE和△B1CF中,
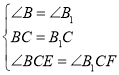 ,
,
∴△BCE≌△B1CF(ASA);
(2)当旋转角等于30°时,AB与A1B1垂直.理由如下:
证明:∵∠ECF=30°,
∴∠BCE=60°,
∴△BCE是等边三角形,
∴∠BEC=60°,得∠A1EO=60°,
又∵∠A1=30°,
∴∠A1EO=60°,
即AB与A1B1垂直.

练习册系列答案
相关题目