题目内容
【题目】如图,点O是等边三角形ABC内的一点,∠AOB=130°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.
(1)判断△COD的形状,并加以说明理由.
(2)若AD=1,OC=![]() ,OA=
,OA=![]() 时,求α的度数.
时,求α的度数.
(3)探究:当α为多少度时,△AOD是等腰三角形?
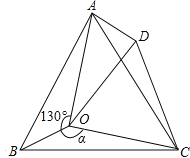
【答案】(1)△COD是等边三角形,理由见解析;(2)α=150°;(3)α为100°、130°、115°时,△AOD为等腰三角形.
【解析】
(1)根据旋转得出CO=CD,∠DCO=60°,根据等边三角形的判定推出即可.
(2)根据三条边的关系得到△AOD为直角三角形,得到∠ADO=90°,从而求出α的值.
(3)用∠α表示∠ADO、∠AOD、∠DAO,分为三种情况:①∠ADO=∠AOD,②∠ADO=∠OAD,③∠OAD=∠AOD,代入求出即可.
(1)∵△ADC≌△BOC,
∴CO=CD,
∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠DCO=60°,
∴△COD是等边三角形.
(2)∵AD=1,OC=![]() ,OA=
,OA=![]()
∴OA2=AD2+OC2
∴△AOD是直角三角形
∴∠ADO=90°
∴α=90°+60°=150°
(3)∠AOD=360°﹣∠AOB﹣∠α﹣∠COD=360°﹣130°﹣∠α﹣60°=170°﹣∠α,
∠ADO=∠ADC﹣∠CDO=∠α﹣60°,
∠OAD=180°﹣∠AOD﹣∠ADO=180°﹣(∠α﹣60°)﹣(170°﹣∠α)=70°,
若∠ADO=∠AOD,即∠α﹣60°=170°﹣∠α,
解得:∠α=115°;
若∠ADO=∠OAD,则∠α﹣60°=70°,
解得:∠α=130°;
若∠OAD=∠AOD,即70°=170°﹣∠α,
解得:∠α=100°;
即当α为100°、130°、115°时,△AOD为等腰三角形.

【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如下表:
购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?