题目内容
【题目】在同一坐标系中,函数y=ax2与y=ax﹣a(a≠0)的图象的大致位置可能是( )
A. 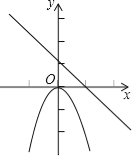 B.
B. 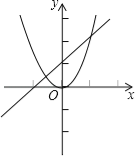 C.
C. 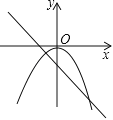 D.
D. 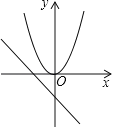
【答案】A
【解析】
试题可先根据a的符号判断一次函数与二次函数的图象所经过的象限,然后作出选择.
解:A、∵一次函数图象经过第二、四象限,∴a<0,
∵y=ax﹣a,则﹣a>0,∴图象与y轴交在y轴正半轴上,
∵二次函数y=ax2的图象的开口方向是向下,∴a<0,故此选项正确;
B、∵一次函数图象经过第一、三象限,∴a>0,
∵y=ax﹣a,∴﹣a<0,∴故图象与y轴交在y轴负半轴上,
∵二次函数y=ax2的图象的开口方向是向上,∴a>0,故此选项错误;
C、∵一次函数图象经过第二、四象限,∴a<0,
∵y=ax﹣a,∴﹣a>0,故图象与y轴交在y轴正半轴上,
∵二次函数y=ax2的图象的开口方向是向下,则a<0,故此选项错误;
D、∵一次函数图象经过第二、四象限,则a<0,
∵y=ax﹣a,∴﹣a>0,∴图象与y轴交在y轴正半轴上,
∵二次函数y=ax2的图象的开口方向是向上,∴a>0,故此选项错误;
故选:A.

练习册系列答案
相关题目