Question

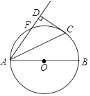
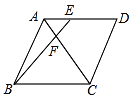
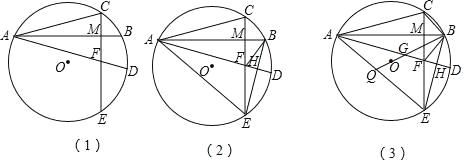
【题目】如图，AB、AC、AD是⊙O的弦，弧BC＝弧BD，CE⊥AB于M，交⊙O于E，交AD于F．

(1)如图1，求证：AF＝AC；

(2)如图2，连接BF、AE、BE，交AD于H，求证：∠DAE＝∠EBF；

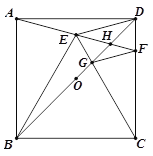
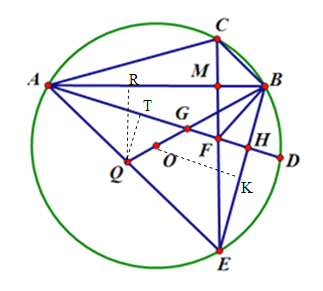
(3)如图3，连接BO，并延长交AE于Q，交AD于点G，连接BC，若QG＝4，FH＝GF，tan∠BCE＝1，求线段AB的长．

Answer 1

【答案】(1)见解析 ；（2）见解析；(3)

【解析】

(1)由ASA证明△AMC≌△AMF，即可得到结论；

(2)证明△ABC≌△AFB，得到∠ACB=∠AFB，进而有∠BCE=∠BFC，根据三角形外角的性质以及圆周角定理即可得到结论；

(3) 过点O作OK⊥BE，过Q作QT⊥AD于T，过Q作QR⊥AB于R．可证△GHB为等腰直角三角形，∠CBA=∠FBA=∠GBH=∠BCE=∠BAE=45°，通过解直角三角形得到QT、AT、AQ、AR、RQ、BR的长，从而得到结论．

(1)∵弧BC=弧BD，CE⊥AB，∴∠BAC=∠BAD，∠AMC=∠AMF=90°．

∵AM=AM，∴△AMC≌△AMF，∴∠ACM=∠AFM，AC=AF．

(2)在△ABC和△AFB中，∵AC=AF，∠BAC=∠BAD，AB=AB，∴△ABC≌△AFB，∴∠ACB=∠AFB．

∵∠ACM=∠AFM，∴∠BCE=∠BFC．

∵∠BCE=∠EAB=∠EAD+∠BAD，∠BFC=∠BEF+∠EBF，∠BEF=∠BAC=∠BAD，∴∠DAE=∠EBF．

(3) 过点O作OK⊥BE，过Q作QT⊥AD于T，过Q作QR⊥AB于R．

∵∠BEC=∠BAC=∠BAD，∠AFM=∠EFH，∴∠EHF=∠AMF=90°．

∵tan∠BCE=1，∴∠BCE=∠BAE=45°．

∵OK⊥BE，∴∠BOK=∠BAE=∠BCE=45°，∴∠OBK=45°，∴∠BGH=45°．

∵∠AHB=90°，∴△GHB为等腰直角三角形．

∵∠TGQ=∠BGH=45°，∠QTG=90°，QG=4，∴QT=．

∵△ABC≌△AFB，∴∠CBA=∠FBA=45°．

∵∠GBH=45°，∴∠ABG=∠FBH．

∵FH=GF，∴tan∠EBF=．

∵∠DAE=∠EBF=∠ABQ，∴tan∠DAE=tan∠TAQ=tan∠ABQ =，∴，，∴AT=2QT=，∴AQ=．

∵∠QAR=∠ECB=45°，∴AR=RQ=，∴BR=2RQ=，∴AB=AR+BR=．